ЬтФПФкШн
ЁОЬтФПЁПдкПкДќжазАга23ИіКХТыЧђЃЌЗжБ№Бъга1~23ЙВ23ИіЪ§зжЃЌИїаЁЧђГ§СЫКХТыВЛЭЌЭтЦфгрЭъШЋЯрЭЌЃЌЯждкДгжаЫцвтШЁГіСНИіаЁЧђЃЌЧѓЃК
ЃЈ1ЃЉЕквЛДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪ;
ЃЈ2ЃЉЕквЛДЮШЁГіЕФаЁЧђКХТыаЁгк30ЕФИХТЪ;
ЃЈ3ЃЉШчЙћЕквЛДЮШЁГіЕФаЁЧђЪЧ3ЃЌВЛЗХЛиЃЌЧѓЕкЖўДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪ;
ЃЈ4ЃЉШчЙћЕквЛДЮШЁГіЕФаЁЧђЪЧ6ЃЌвВВЛЗХЛиЃЌдйЧѓЕкЖўДЮШЁГіЕФаЁЧђКХТыЪЧХМЪ§ЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕквЛДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪЮЊ![]() ЃЛЃЈ2ЃЉЕквЛДЮШЁГіЕФаЁЧђКХТыаЁгк30ЕФИХТЪЮЊ1ЃЛЃЈ3ЃЉЕкЖўДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪЮЊ
ЃЛЃЈ2ЃЉЕквЛДЮШЁГіЕФаЁЧђКХТыаЁгк30ЕФИХТЪЮЊ1ЃЛЃЈ3ЃЉЕкЖўДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪЮЊ![]() ЃЛЃЈ4ЃЉЕкЖўДЮШЁГіЕФаЁЧђКХТыЪЧХМЪ§ЕФИХТЪЮЊ
ЃЛЃЈ4ЃЉЕкЖўДЮШЁГіЕФаЁЧђКХТыЪЧХМЪ§ЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
НтЃК(1)гЩЬтвтжЊЃКдк1~23жаЃЌДѓгк9ЕФга10~23ЙВ14ИіЪ§зжЃЌ
дђЕквЛДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
(2)вђЮЊКХТыШЋВПаЁгк30ЃЌ
ЙЪЕквЛДЮШЁГіЕФаЁЧђКХТыаЁгк30ЕФИХТЪЮЊ1ЃЛ
(3)ШЁГівЛИіаЁЧђ3КѓЃЌДѓгк9ЕФШдга10~23ЙВ14ИіЪ§зжЃЌ
дђЕкЖўДЮШЁГіЕФаЁЧђКХТыДѓгк9ЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
(4)ШЁГівЛИіаЁЧђ6КѓЃЌЪЃЯТЕФаЁЧђжаЃЌаЁЧђКХТыЪЧХМЪ§ЕФга10ИіЃЌ
дђЕкЖўДЮШЁГіЕФаЁЧђКХТыЪЧХМЪ§ЕФИХТЪЮЊ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
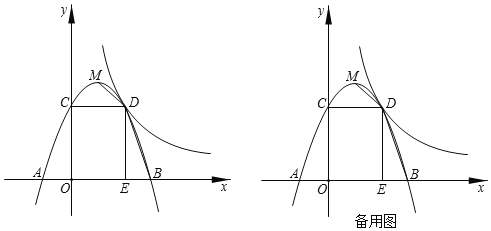
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГЬхг§гУЦЗЩЬЕъЮЊСЫНт3дТЗнЕФЯњЪлЧщПіЃЌЖдБОдТИїРрЩЬЦЗЕФЯњЪлЧщПіНјааЕїВщЃЌВЂНЋЕїВщЕФНсЙћЛцжЦГЩШчЯТЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
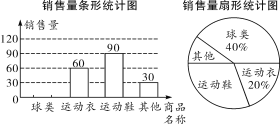
ЃЈ1ЃЉЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНЋЬѕаЮЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉИУЩЬЕъзМБИАД3дТЗнЧђРрЩЬЦЗЯњЪлСПЙКНјЧђРрЩЬЦЗЃЌКЌРКЧђЁЂзуЧђЁЂХХЧђШ§жжЃЌдЄМЦЧЁКУгУЭъНјЛѕПюЙВ3600дЊЃЌЩшЙКНјРКЧђxИіЃЌзуЧђyИіЃЌШ§жжЧђЕФНјМлКЭЪлМлШчЯТБэЃК
РрБ№ | РКЧђ | зуЧђ | ХХЧђ |
НјМлЃЈЕЅЮЛЃКдЊ/ИіЃЉ | 50 | 30 | 20 |
дЄЪлМлЃЈЕЅЮЛЃКдЊ/ИіЃЉ | 70 | 45 | 25 |
ЧѓyгыxжЎМфТњзуЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉИУЩЬЕъзлКЯПМТЧИїжжвђЫиЃЌдЄМЦУПжжЧђЯњЪлГЌЙ§60ИіКѓЃЌетжжЧђОЭЛсВњЩњжЭЯњЃЎ
ЂйМйЩшЫљЙКНјРКЧђЁЂзуЧђЁЂХХЧђФмШЋВПЪлГіЃЌЧѓГідЄЙРРћШѓPЃЈдЊЃЉгыxЃЈИіЃЉжЎМфТњзуЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЧѓГідЄЙРРћШѓЕФзюДѓжЕЃЌВЂаДГіДЫЪБЙКНјШ§жжЧђИїЖрЩйИіЃЎ
ЁОЬтФПЁПФГЙЋЫОЙВ20УћдБЙЄЃЌдБЙЄЛљБОЙЄзЪЕФЦНОљЪ§ЮЊ2200дЊЃЎЯжОЭЦфИїИкЮЛУПШЫЕФЛљБОЙЄзЪЧщПіКЭИїИкЮЛШЫЪ§ЃЌЛцжЦСЫЯТСаЩаВЛЭъећЕФЭГМЦЭМБэЃКИїИкЮЛУПШЫЕФЛљБОЙЄзЪЧщПіЭГМЦБэ
ИкЮЛ | ОРэ | ММЪІ | СьАр | жњРэ | ЗўЮёдБ | ЧхНрЙЄ |
ЛљБОЙЄзЪ | 10000 | 4000 | 2400 | 1600 | 1000 |
ЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЋИїИкЮЛШЫЪ§ЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЧѓИУЙЋЫОЗўЮёдБУПШЫЕФЛљБОЙЄзЪЃЛ
ЃЈ3ЃЉИУЙЋЫОЫљгадБЙЄЛљБОЙЄзЪЕФжаЮЛЪ§ЪЧ дЊЃЌжкЪ§ЪЧ дЊЃЛФуШЯЮЊгУЛљБОЙЄзЪЕФЦНОљЪ§КЭжаЮЛЪ§РДДњБэИУЙЋЫОдБЙЄЛљБОЙЄзЪЕФвЛАуЫЎЦНЃЌФФвЛИіИќЧЁЕБЃПЧыЫЕУїРэгЩЃЎ
ЃЈ4ЃЉИУЙЋЫОвЛУћдБЙЄЯђОРэДЧжАСЫЃЌШєЦфЫћдБЙЄЕФЛљБОЙЄзЪВЛБфЃЌФЧУДЛљБОЙЄзЪЕФЦНОљЪ§ОЭНЕЕЭСЫЃЎФуШЯЮЊДЧжАЕФПЩФмЪЧФФИіИкЮЛЩЯЕФдБЙЄФиЃПЫЕУїРэгЩЃЎ