题目内容
【题目】某药店销售口罩,进价15元,售价20元,为防控新冠肺炎疫情,药店决定凡是一次性购买10个以上的客户,每多买一个,售价就降低0.1元(顾客所购买的全部口罩),但最低价是17元/个.
(1)顾客一次性至少购买多少个口罩时,才能以最低价17元/个购买?
(2)写出一次性购买x个口罩时(x>10),药店的利润y(元)与购买量x(个)之间的函数关系式;
(3)在销售过程中,药店发现一次性卖出36个口罩时比卖出26个口罩的钱少,为了使每次销售均能达到多卖就能多获利,在其他促销条件不变的情况下,最低价应确定为每个多少元?
【答案】(1)顾客一次性至少购买40个口罩时,才能以最低价17元/个购买;(2)y=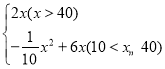 ;(3)最低价应确定为每个18元.
;(3)最低价应确定为每个18元.
【解析】
(1)设顾客一次性至少购买x个口罩时,才能以最低价17元/个购买,由题意得关于x的一元一次方程,解方程即可;
(2)分两种情况:①当x>40时;②当10<x≤40时,分别写出函数关系式即可;
(3)当10<x≤40时,将函数关系式配方,根据二次函数的性质及问题的实际意义可得答案.
解:(1)设顾客一次性至少购买x个口罩时,才能以最低价17元/个购买,由题意得:
20﹣(x﹣10)×0.1=17,
解得x=40.
∴顾客一次性至少购买40个口罩时,才能以最低价17元/个购买.
(2)当x>40时,y=(17﹣15)x=2x;
当10<x≤40时,y=[(20﹣15)﹣(x﹣10)×0.1]x=﹣![]() x2+6x.
x2+6x.
∴药店的利润y购买量x之间的函数关系式为y=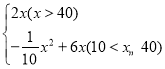 .
.
(3)当10<x≤40时,
y=﹣![]() x2+6x
x2+6x
=﹣![]() (x﹣30)2+90.
(x﹣30)2+90.
∵二次项系数﹣![]() <0,
<0,
∴当x=30时,y有最大值,且30<x≤40,y随x的增大而减小,
∴最低价应定在销售量为30个时的价格,才能使每次销售均能达到多卖就能多获利,
此时最低价为:20﹣(30﹣10)×0.1=18(元).
∴最低价应确定为每个18元.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 9 | 8 | 8 | 7 |
乙 | 10 | 6 | 7 | 9 |
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩;
(2)分别计算甲、乙两人四次测试成绩的方差;根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
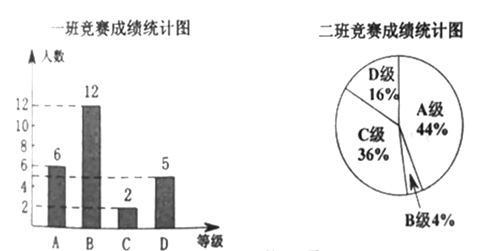
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)