题目内容
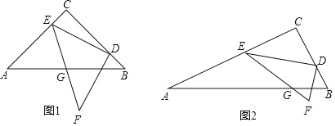
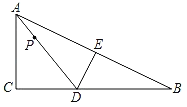
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P在线段AD上,当点P到△ABC的直角边距离等于5时,AP的长为_____.
【答案】![]() 或
或![]() .
.
【解析】
设BD=x,由折叠性质得AD与CD;再由勾股定理列出x的方程,进而求得DC的长;然后再分两种情况:①点P到AC边的距离等于5时、②当点P到BC边的距离等于5时,过P作△ABC直角边的垂线段,最后根据相似三角形的性质求解即可.
解:设BD=x,由折叠知AD=BD=x,CD=16﹣x,
在Rt△ACD中,由勾股定理得,x2=82+(16﹣x)2,
解得,x=10,
∴BD=10,CD=6,
分两种情况:①点P到AC边的距离等于5时,过点P作PF⊥AC于点F,如图1,
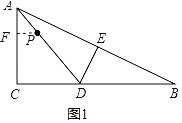
∴PF=5,PF∥CD,
∴△APF∽△ADC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AP=![]() ;
;
②当点P到BC边的距离等于5时,过点P作PG⊥BC于点G,如图2,
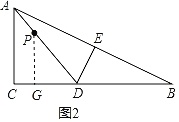
∴PG=5,PG∥AC,
∴△DPG∽△DAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴DP=![]() ,
,
∴AP=10﹣![]() =
=![]() ,
,
综上,AP的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?