题目内容
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是时,它们一定不全等.
【答案】钝角三角形或直角三角形;钝角三角形
【解析】解:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1 , BC=B1C1 , ∠C=∠C1 .
求证:△ABC≌△A1B1C1 .
证明:过B作BD⊥AC于D,过B1作B1D1⊥A1C1于D1 ,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,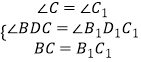 ,
,
∴△BDC≌△B1D1C1 ,
∴BD=B1D1 ,
在Rt△BDA和Rt△B1D1A1中![]() ,
,
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1 ,
在△ABC和△A1B1C1中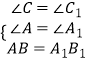 ,
,
∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是钝角三角形或直角三角形时,它们也会全等,
如图:△ACD与△ACB中,
CD=CB,AC=AC,∠A=∠A,
但:△ACD与△ACB不全等. ,
,
故当这两个三角形其中一个三角形是锐角三角形,另一个是钝角三角形时,它们一定不全等.
故答案为:钝角三角形或直角三角形,钝角三角形.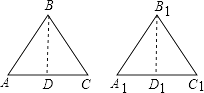
过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1 , 得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,根据SAS证△BDC≌△B1D1C1 , 推出BD=B1D1 , 根据HL证Rt△BDA≌Rt△B1D1A1 , 推出∠A=∠A1 , 根据AAS推出△ABC≌△A1B1C1即可.本题考查了全等三角形像的判定;SSA不能判定的原因是有锐角钝角三角形不能全等,把三角形分类后就能全等了.