Question

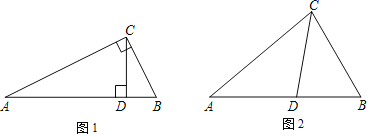
【题目】两个大小不同的等腰直角三角形三角板如图所示放置，图是由它抽象出的几何图形，B，C，E在同一条直线上，联结DC，

请找出图中的全等三角形，并给予说明说明：结论中不得含有未标识的字母；

试说明：．

Answer 1

【答案】⑴△≌△证明略 ⑵略

【解析】

试题①可以找出△BAE≌△CAD，条件是AB=AC，DA=EA，∠BAE=∠DAC=90°+∠CAE．

②由①可得出∠DCA=∠ABC=45°，则∠BCD=90°，所以DC⊥BE．

解：（1）∵△ABC，△DAE是等腰直角三角形，

∴AB=AC，AD=AE，∠BAC=∠DAE=90°．

∠BAE=∠DAC=90°+∠CAE，

在△BAE和△DAC中

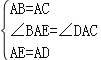
∴△BAE≌△CAD（SAS）．

（2）由（1）得△BAE≌△CAD．

∴∠DCA=∠B=45°．

∵∠BCA=45°，

∴∠BCD=∠BCA+∠DCA=90°，

∴DC⊥BE．