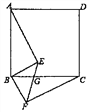
[题目]如图.等腰直角△ABC中.∠BAC=90°.BC=6.过点C作CD⊥BC.CD=2.连接BD.过点C作CE⊥BD.垂足为E.连接AE.则AE长为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，等腰直角△ABC中，∠BAC=90°，BC=6，过点C作CD⊥BC，CD=2，连接BD，过点C作CE⊥BD，垂足为E，连接AE，则AE长为_____．

【答案】

【解析】根据旋转的性质得到△ABF≌△ACE，进而得出△AEF为等腰直角三角形，根据两角对应相等的两三角形相似的判定可得△BCD∽△BEC，然后根据对应边成比例可得，然后根据勾股定理即可求解.

把AE逆时针旋转90°，使AE=AF交BD于F，

根据旋转的性质可得△ABF≌△ACE，

即BF=CE，

∴△AEF是等腰直角三角形

∵CD⊥BC，CE⊥BD

∴∠BCD=∠CEB=90°

∵∠DBC=∠CBD，

∴△BCD∽△BEC

∴

∵BC=6，CD=2

∴BD==

即CE=

∴DE=

即BE=

∴EF=——=

∴AE=AF=

故答案为：.

练习册系列答案

(1)求a的值；

(2)求一次函数的解析式并画出它的图象；

(3)若P(m，y1)，Q(m－1，y2)是这个一次函数图象上的两点，试比较y1与y2的大小．

【题目】如图，AOC=，ON是锐角COD的角平分线，OM是AOC的角平分线，那么，MON= （）

A. COD+ B.

C. AOD D.

【题目】如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G.

(1)求证：AE=CF；

(2)若∠ABE=55°，求∠EGC的大小．

【题目】如图，已知在△ABC中，AB＞AC，BE，CF都是△ABC的高线，P是BE上一点，且BP＝AC，Q是CF延长线上一点，且CQ＝AB，连结AP，AQ，QP.求证：

(1)AQ＝PA.

(2)AP⊥AQ.

【题目】如图，AB是圆O的直径，C，D是圆O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F．则下列结论：
①AD⊥BD；②∠AOC=∠ABC；③CB平分∠ABD；④AF=DF；⑤BD=2OF．
其中一定成立的是（）

A.①③⑤
B.②③④
C.②④⑤
D.①③④⑤

【题目】在数轴上，点A表示数a，点B表示数b，已知a、b满足.

（1）求a、b的值；

（2）若在数轴上存在一点C，使得C到A的距离是C到B的距离的2倍，求点C表示的数；

（3）若小蚂蚁甲从点A处以1个单位长度/秒的速度向左运动，同时小蚂蚁乙从点B处以2个单位长度/秒的速度也向左运动，丙同学观察两只小蚂蚁运动，在它们刚开始运动时在原点O处放置一颗饭粒，乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动，设运动的时间为t秒．求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t．