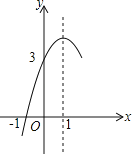题目内容
【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装怖品商店,该店采购了一种今年新上市的装饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件),销售价格Q(元/件)与销售时间x(天) (1≤x≤30,且x为正整数)都满足一次函数关系,其函数图象如图所示:
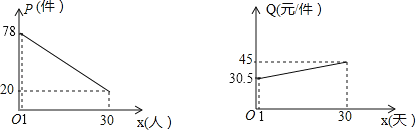
(1)请直接写出:销售量(P件)与销售时间x(天)之间的函数关系式,销售价格Q(元/件)与销售时间x(天)之间的函数关系式;
(2)请问在30天的试销售中,哪﹣天的日销售利润最大?求最大利润.
【答案】(1)P=﹣2x+80;Q=![]() x+30;(2)在30天的试销售中,第10天的日销售利润最大,最大利润为900元.
x+30;(2)在30天的试销售中,第10天的日销售利润最大,最大利润为900元.
【解析】
(1)根据图象利用待定系数法确定一次函数的解析式即可;
(2)根据题意列出有关销售利润的函数关系式求得最值即可.
(1)设p=ax+b,q=cx+d,
根图象知:
![]() ,
,![]()
解得:![]() ,
,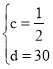 ,
,
∴P=﹣2x+80;Q=![]() x+30,
x+30,
故答案为:P=﹣2x+80;Q=![]() x+30;
x+30;
(2)设30天的试销售中,每天的销售利润为W元,则
W=P(Q﹣20)=(﹣2x+80)[(![]() x+30)﹣20]
x+30)﹣20]
=﹣x2+20x+800
∵W=﹣(x﹣10)2+900.
所以当x=10时,W有最大值,W的最大值为900.
所以在30天的试销售中,第10天的日销售利润最大,最大利润为900元.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目