题目内容
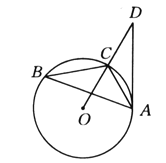
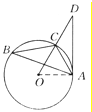
【题目】如图所示，已知△ABC内接于⊙O，点D在OC的延长线上，sin B＝
，∠D＝30°．
(1)求证AD是⊙O的切线；
(2)若AC＝6，求AD的长．
【答案】(1) 证明见解析； (2) 
．
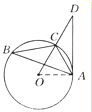
【解析】试题分析：（1）要证明AD是⊙O的切线，只要证明∠OAD=90°即可；
（2）根据已知可得△AOC是等边三角形，从而得到OA=AC=6，则可以利用勾股定理求得AD的长．
解：(1) 如图所示，连接OA．∵sin B＝
，∴∠B＝30°，∴∠AOC＝60°．∵∠D＝30°，∴∠OAD＝180°－∠D－∠AOD＝90°．∴AD是⊙O的切线．
(2)∵OA＝OC，∠AOC＝60°，∴△AOC是等边三角形．∴OA＝AC＝6．∵∠OAD＝90°，∠D＝30°，∴AD＝
．
练习册系列答案
相关题目
