题目内容
【题目】问题探究:
(一)(新知学习):圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
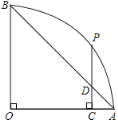
(二)(问题解决):已知⊙O的直径为4,AB,CD是⊙O的直径.P是![]() 上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.



(1)若直径AB⊥CD,点P为![]() 上一动点(不与B、C重合)(如图一).
上一动点(不与B、C重合)(如图一).
① 证明:四边形PMON内接于某圆;②证明MN的长为定值,并求其定值;
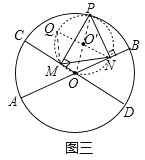
(2)若直径AB与CD相交成120°角.
① 当点P运动到![]() 的中点时(如图二),求MN的长;
的中点时(如图二),求MN的长;
② 当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(3)试问当直径AB与CD相交角∠BOC=______度时,MN的长取最大值,其最大值为_____.
【答案】(1)①见解析,②见解析;(2)①![]() ,②MN是定值;(3)当直径AB与CD相交成90°角时,MN取得最大值2.
,②MN是定值;(3)当直径AB与CD相交成90°角时,MN取得最大值2.
【解析】
(1)如图一,易证∠PMO+∠PNO=180°,从而可得四边形PMON内接于圆;②易证四边形PMON是矩形,则有MN=OP=2,问题得以解决;
(2)①如图二,根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°,根据圆内接四边形的对角互补可得∠MP1N=60°.根据角平分线的性质可得P1M=P1N,从而得到△P1MN是等边三角形,则有MN=P1M.然后在Rt△P1MO中运用含30°直角三角形的性质即可解决问题;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,根据圆周角定理可得∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中运用含30°直角三角形的性质可得MQ=1,然后利用勾股定理即可解决问题;
(4)由MN是直径为OP的圆内的一条弦,根据圆中最长的弦是直径,进行分析解答即可.
解:(1)①如图一,
∵PM⊥OC,PN⊥OB,
∴∠PMO=∠PNO=90°,
∴∠PMO+∠PNO=180°,
∴四边形PMON内接于圆;
②如图一,
∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,
∴MN=OP=2,
∴MN的长为定值,该定值为2;

(2)①如图二,
∵P1是![]() 的中点,∠BOC=120°
的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,
∴P1M=P1N,∠MP1O=30°,
∴△P1MN是等边三角形,
∴MN=P1M.
∵OM=![]() P1O=1
P1O=1
∴P1M=![]() ,
,
∴MN=![]() ;
;

②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,
则有∠QMN=90°,∠MQN=∠MPN=60°,
∴∠MNQ=30°,
在Rt△QMN中,MQ=![]() NQ=1
NQ=1
∴MN=![]()
∴MN是定值.
(3)由题意可知,MN是直径为OP=2的圆内的一条弦,
∴MN的最大值为2,
∴当∠BOC=90°时,在矩形PMON中,MN=OP=2,
即当直径AB与CD相交角∠BOC=90°时,MN的长取最大值,其最大值为2.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级: 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级: 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据______来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;