题目内容
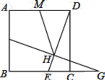
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 上一点.点
上一点.点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在
恰好在![]() 延长线上,
延长线上,![]() 交
交![]() 于点
于点![]() .点
.点![]() 为
为![]() 的中点,若
的中点,若![]() ,则
,则![]() =_____.
=_____.
【答案】5
【解析】
连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,由点F,点G关于直线DE的对称,得到DF=DG,根据正方形的性质得到AD=CD,∠ADC=∠A=∠BCD=90°,推出Rt△AFD≌Rt△CDG,证得△FDG是等腰直角三角形,推出四边形APHQ是矩形,证得△HPF≌△DHQ,根据全等三角形的性质得到HP=HQ,证得APHQ为正方形,利用正方形性质联系题中所给数据计算出正方形边长,然后再利用△FPH∽△EHG求得EG长.
解:连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,

∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,
∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,
![]()
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
![]()
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,
又在△PFF与△DQH中有:
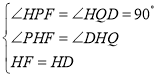
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,
则有![]() ,即
,即![]() ,
,
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级: 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级: 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据______来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共10只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
(2)试估算口袋中黑、白两种颜色的球各有多少只?
(3)请画树状图或列表计算:从中一次摸两只球,这两只球颜色不同的概率是多少?