题目内容
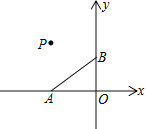
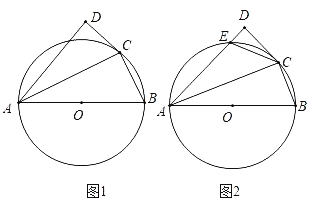
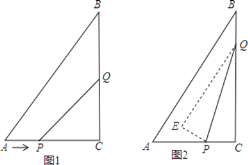
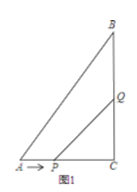
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的 速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
(1)当t= 时,PQ∥AB
(2)当t为何值时,△PCQ的面积等于5cm2?
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
【答案】(1)2.4;(2)1;(3)见解析.
【解析】
(1)由PQ∥AB得出△PQC∽△ABC,从而得到比例式PC:AC=CQ:BC,建立关于t的方程,解方程求出t的值即可;
(2)由三角形面积公式可建立关于t的方程,解方程求出t的值即可;
(3)延长QE交AC于点D,若PE⊥AB,则QD∥AB,所以可得△CQD∽△CBA,由相似三角形的性质:对应边的比值相等可求出DE=0.5t,易证△ABC∽△DPE,再由相似三角形的性质可得![]() ,把已知数据代入即可求出t的值.
,把已知数据代入即可求出t的值.
解:(1) ∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴PC=AC-AP=6-t,CQ=2t,
当PQ∥AB时,∴△PQC∽△ABC,
∴PC:AC=CQ:BC,
∴(6-t):6=2t:8
∴t=2.4
∴当t=2.4时,PQ∥AB
(2)∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴PC=AC-AP=6-t,CQ=2t,
∴S△CPQ=![]() CPCQ=
CPCQ=![]() =5,
=5,
∴t2-6t+5=0
解得t1=1,t2=5(不合题意,舍去)
∴当t=1秒时,△PCQ的面积等于5cm2;
(3)能垂直,理由如下:
延长QE交AC于点D,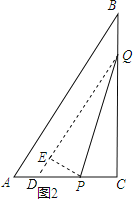
∵将△PQC翻折,得到△EPQ,
∴△QCP≌△QEP,
∴∠C=∠QEP=90°,
若PE⊥AB,则QD∥AB,
∴△CQD∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴QD=2.5t,
∵QC=QE=2t
∴DE=0.5t
∵∠A=∠EDP,∠C=∠DEP=90°,
∴△ABC∽△DPE,
∴![]()
∴![]() ,
,
解得:![]() ,
,
综上可知:当t=![]() 时,PE⊥AB.
时,PE⊥AB.

 阅读快车系列答案
阅读快车系列答案【题目】中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级: 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级: 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
(1)根据上面的数据,将下列表格补充完整,整理、描述数据:
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
(2)为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据______来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);
(3)若八年级有800名学生,试估计八年级学生成绩优秀的人数;