题目内容
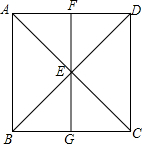
如图,已知正方形ABCD的边长为a,AC与BD交于点E,过点E作FG∥AB,且分别交AD、BC于点F、G.问:以B为圆心,
a为半径的圆与直线AC、FG、DC的位置关系如何?
| ||
| 2 |

∵四边形ABCD是正方形,
∴EA=EB=EC=ED,AC⊥BD,∠ABC=∠BCD=90°,
∵FG∥AB,
∴BG=GC=
BC=
a,AF=DF=
a,∠EGB=90°,
在Rt△ABE中,由勾股定理得:2AE2=a2,
AE=
a=BE,
∵BE=
a,BE⊥AC,∴以B为圆心,
a为半径的圆与直线AC的位置关系是相切;
∵BG=
a<
a,BG⊥FG,
∴以B为圆心,
a为半径的圆与直线FG的位置关系是相交;
∵BC=a,BC⊥CD,
∴以B为圆心,
a为半径的圆与直线DC的位置关系是相离.
∴EA=EB=EC=ED,AC⊥BD,∠ABC=∠BCD=90°,
∵FG∥AB,
∴BG=GC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABE中,由勾股定理得:2AE2=a2,
AE=
| ||
| 2 |
∵BE=
| ||
| 2 |
| ||
| 2 |
∵BG=
| 1 |
| 2 |
| ||
| 2 |
∴以B为圆心,
| ||
| 2 |
∵BC=a,BC⊥CD,
∴以B为圆心,
| ||
| 2 |

练习册系列答案
相关题目
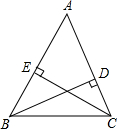
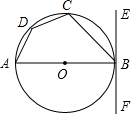
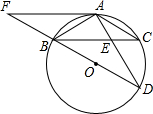 点E,AE=2,ED=4.
点E,AE=2,ED=4.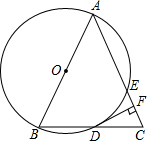

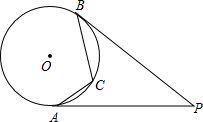
 45°.
45°.