Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ“ĽłĪ»żĹ«įŚĶńŃĹŅť»żĹ«įŚĶń»żłŲĹ«∂» ż∑÷Īūő™90°„°Ę60°„°Ę30°„ļÕ90°„°Ę45°„°Ę45°„£¨ő“√«Ņ…“‘”√»żĹ«įŚĶńĹ«∆ī≥Ų“Ľ–©Őō ‚∂» żĶńĹ«£ģ
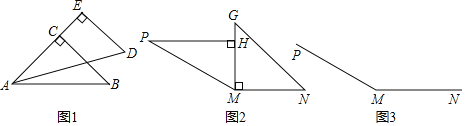
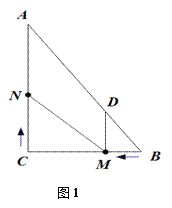
£®1£©ŃĹŅť»żĹ«įŚįī»ÁÕľ1ňý ĺ∆īĹ”£¨‘Ú°ŌBADĶń∂» ż «°° °°°„£ģ
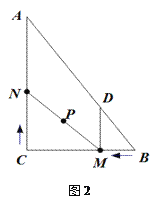
£®2£©–°√ų”√ŃĹŅť»żĹ«įŚįīÕľ2∆ī≥ŲĶń°ŌPMNĶń∂» ż «°° °°°„£ģ
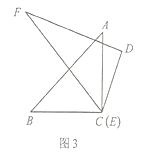
£®3£©–°√ųŌŽĽ≠≥ŲÕľ2∆ī≥ŲĶń°ŌPMNĶńĹ«∆Ĺ∑÷ŌŖ£¨«Žń„÷Ľ”√“ĽłĪ»żĹ«įŚ‘ŕÕľ3÷–įÔ–°√ųÕÍ≥…Ľ≠Õľ£ģ£®≤Ľ–īĽ≠∑®£¨Ī£ŃŰĽ≠ÕľļŘľ££¨ĪÍ≥ŲĪō“™Ķń∂» ż£©
°ĺīūįł°Ņ£®1£©15£Ľ£®2£©150£Ľ£®3£©ľŻĹ‚őŲ
°ĺĹ‚őŲ°Ņ
£®1£©ŃĹŅť»żĹ«įŚįī»ÁÕľ1ňý ĺ∆īĹ”£¨Ķ√°ŌBADĶń∂» ż « 45°„©Ā30°„=15°„£ģ
£®2£©ŃĹŅť»żĹ«įŚįīÕľ2∆ī≥ŲĶń°ŌPMNĶń∂» ż «90°„+60°„=150°„£ģ
£®3£©Ľ≠≥ŲÕľ2∆ī≥ŲĶń°ŌPMNĶńĹ«∆Ĺ∑÷ŌŖ£¨”√“ĽłĪ»żĹ«įŚĶń45∂»Ĺ«ľ”…Ō30∂»Ĺ«ľīŅ…‘ŕÕľ3÷–ÕÍ≥…Ľ≠Õľ£ģ
Ĺ‚£ļ»ÁÕľňý ĺ£ļ
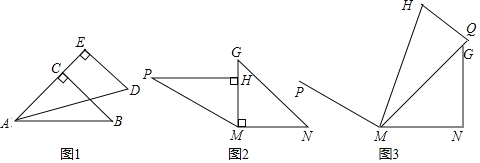
£®1£©»ÁÕľ1£¨Ķ√£ļ°ŌBAD= °ŌBAC°ŌDAE=45°„©Ā30°„=15°„£¨
Ļ īūįłő™£ļ15£Ľ
£®2£©»ÁÕľ2£¨Ķ√£ļ°ŌPMN=°ŌGMN+°ŌPMH =90°„+60°„=150°„,
Ļ īūįłő™£ļ150£Ľ
£®3£©”…£®2£©Ņ…÷™°ŌPMN=150°„,
łýĺ›Ĺ«∆Ĺ∑÷ŌŖĶń∂®“Ś£¨°ŌPMNŅ…∑÷ő™∂» ż∂ľ «75°„ĶńŃĹłŲĹ«£¨
‘Ú”√“ĽłĪ»żĹ«įŚĶń45∂»Ĺ«ľ”…Ō30∂»Ĺ«ľīŅ…Ķ√≥Ų75°„£¨
ňý“‘”√“ĽłĪ»żĹ«įŚĶń45∂»Ĺ«ľ”…Ō30∂»Ĺ«ľīŅ…‘ŕÕľ3÷–ÕÍ≥…Ľ≠Õľ£ģ

°ĺŐ‚ńŅ°ŅľÚĶ•∂ŗ√śŐŚ «łųłŲ√ś∂ľ «∂ŗĪŖ–ő◊ť≥…ĶńľłļőŐŚ£¨ ģįň ņľÕ»ū Ņ ż—ßľ“Ň∑ņ≠÷§√ųŃňľÚĶ•∂ŗ√śŐŚ÷–∂•Ķ„ ż£®V£©°Ę√ś ż£®F£©ļÕņ‚ ż£®E£©÷ģľšīś‘ŕ“ĽłŲ”–»§ĶńĻōŌĶ Ĺ£¨≥∆ő™Ň∑ņ≠Ļę Ĺ£ģ»ÁĪŪ «łýĺ›◊ůĪŖĶń∂ŗ√śŐŚń£–ÕŃ–≥ŲĶń≤ĽÕÍ’ŻĶńĪŪ£ļ
∂ŗ√śŐŚ | ∂•Ķ„ ż | √ś ż | ņ‚ ż |
ňń√śŐŚ | 4 | 4 | 6 |
≥§∑ĹŐŚ | 8 | 6 | |
’żįň√śŐŚ | 8 | 12 |
Ō÷‘ŕ”–“ĽłŲ∂ŗ√śŐŚ£¨ňŁĶń√Ņ“ĽłŲ√ś∂ľ «»żĹ«–ő£¨ňŁĶń√ś ż£®F£©ļÕņ‚ ż£®E£©ĶńļÕő™30£¨‘Ú’‚łŲ∂ŗ√śŐŚĶń∂•Ķ„ żV£Ĺ_____£ģ