题目内容
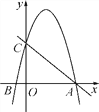
【题目】如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴,y轴分别交于点A,C两点,二次函数y=-x2+bx+c的图象经过点A,点B.
(1)求这个二次函数的解析式;
(2)点P是该二次函数图象的顶点,求△APC的面积;
(3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标.
【答案】(1)y=-x2+4x+5;(2) 15;(3) Q点坐标为![]() 或(2,3)
或(2,3)
【解析】(1)、根据一次函数得出点A和点C的坐标,然后利用待定系数法求出二次函数的解析式;(2)、首先根据二次函数得出点P的坐标,过点P作PD∥y轴交AC于点D,将三角形分成两个三角形来进行计算;(3)、根据三角形相似,分两种情况来进行计算,分别得出点Q的坐标.
(1)∵一次函数y=-x+5的图象与x轴,y轴分别交于A,C两点,
∴A(5,0),C(0,5).∵二次函数y=-x2+bx+c的图象经过点A,点B,
∴b=4,c=5,∴二次函数的解析式为y=-x2+4x+5;
(2)∵y=-x2+4x+5=-(x-2)2+9,∴P(2,9).
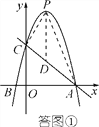
过点P作PD∥y轴交AC于点D,如答图①,则D(2,3).
∴S△APC=![]() (xA-xC)(yP-yD)=15;
(xA-xC)(yP-yD)=15;
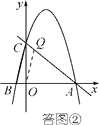
(3)①若△ABC∽△AOQ,如答图②,此时,OQ∥BC.
由B,C两点坐标可求得BC的解析式为y=5x+5. ∴OQ的解析式为y=5x.
由![]() 解得
解得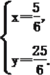 ∴Q
∴Q![]() ;
;
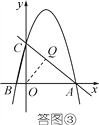
②若△ABC∽△AQO,如答图③,此时,![]() =
=![]() .
.
∵AB=6,AO=5,AC=5![]() ,∴AQ=3
,∴AQ=3![]() ,∴Q(2,3).
,∴Q(2,3).
综上所述,满足要求的Q点坐标为![]() 或(2,3).
或(2,3).

【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?