题目内容
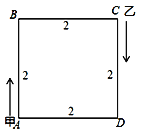
【题目】如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=_____,CH=_____.
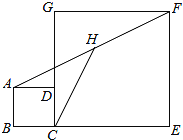
【答案】10, 5.
【解析】
根据正方形的性质求出AB=BC=1,CE=EF=7,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=8,FM=6,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=![]() AF,根据勾股定理求出AF即可.
AF,根据勾股定理求出AF即可.
∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=7,
∴AB=BC=1,CE=EF=7,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+7=8,FM=EF﹣AB=7﹣1=6,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=![]() AF,
AF,
在Rt△AMF中,由勾股定理得:AF=![]() =
=![]() =10,
=10,
∴CH=5,
故答案为:10,5.

练习册系列答案
相关题目
【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?