Question

如图所示，在边长为2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长最小值为cm（结果保留准确值）．

Answer 1

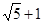
试题考查知识点：正方形的对称性；两点间线段最短。
思路分析：想办法把随动点移动而变化的线段转移到同一条线段上，有利于求和。
具体解答过程：
如图所示，连接PE，E是CD的中点。

∵四边形ABCD是正方形，AC是对角线
∴正方形ABCD关于AC所在的直线对称，PQ=PE，∠BCE=90°
∵BE两点间线段最短
∴当B、P、E三点在同一直线上时，BP+PE的和最小
∵Q是BC的中点，正方形ABCD的边长为2cm
∴BQ=BC=×2cm=1cm,CE=CD=×2cm=1cm
BP+PE和的最小值即BE===cm
∴△PBQ周长的最小值为L=BQ+BP+QP=BE+BQ=(+1)cm
试题点评：求两条线段和的最小值往往离不开“两点间线段最短”。