Question

【题目】已知Rt△AEC中，∠E＝90°，请按如下要求进行操作和判断：

（1）尺规作图：作△AEC的外接圆⊙O，并标出圆心O（不写画法）；

（2）延长CE，在CE的延长线上取点B，使EB＝EC，连结AB，设AB与⊙O的交点为D（标出字母B、D），判断：图中与相等吗？请说明理由.

Answer 1

【答案】(1)作图见解析；（2）证明见解析.

【解析】试题分析：（1）先作出AC的中垂线，交AC于O，再以O为圆心，AO的长为半径画圆即可；
（2）延长CE，在CE的延长线上取点B，使EB=EC，连结AB，先判定△AEC≌△AEB（SAS），得出∠CAE=∠DAE即可得出结论．

试题解析：（1）如图所示，⊙O即为所求；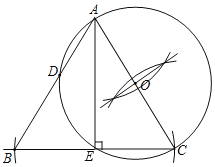

（2）延长CE，在CE的延长线上取点B，使EB=EC，连结AB，则△AEB即为所求，
∵BE=EC，AE=AE，AE⊥BC，
∴△AEC≌△AEB（SAS），
∴∠CAE=∠DAE，
∴相等．