Ő‚ńŅńŕ»›
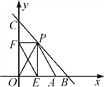
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™∂ĢīőļĮ ży=©Āx2+bx+c£®b£¨cő™≥£ ż£©ĶńÕľŌůĺ≠ĻżĶ„A£®3£¨1£©£¨Ķ„C£®0£¨4£©£¨∂•Ķ„ő™Ķ„M£¨ĻżĶ„A◊ųAB°őx÷Š£¨ĹĽy÷Š”ŕĶ„D£¨ĹĽł√∂ĢīőļĮ żÕľŌů”ŕĶ„B£¨Ń¨ĹŠBC£ģ
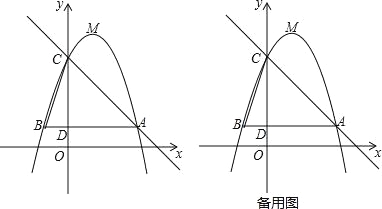
£®1£©«ůł√∂ĢīőļĮ żĶńĹ‚őŲ ĹľįĶ„MĶń◊ÝĪÍ£Ľ
£®2£©»ŰĹęł√∂ĢīőļĮ żÕľŌůŌÚŌ¬∆Ĺ“∆m£®m£ĺ0£©łŲĶ•őĽ£¨ Ļ∆Ĺ“∆ļůĶ√ĶĹĶń∂ĢīőļĮ żÕľŌůĶń∂•Ķ„¬š‘ŕ°ųABCĶńńŕ≤Ņ£®≤ĽįŁņ®°ųABCĶńĪŖĹÁ£©£¨«ůmĶń»°÷Ķ∑∂őߣĽ
£®3£©Ķ„P «÷ĪŌŖAC…ŌĶń∂ĮĶ„£¨»ŰĶ„P£¨Ķ„C£¨Ķ„MňýĻĻ≥…Ķń»żĹ«–ő”Ž°ųBCDŌŗň∆£¨«Ž÷ĪĹ”–ī≥Ųňý”–Ķ„PĶń◊ÝĪÍ£®÷ĪĹ”–ī≥ŲĹŠĻŻ£¨≤ĽĪō–īĹ‚īūĻż≥Ő£©£ģ
°ĺīūįł°Ņ£®1£©y=©Āx2+2x+4£ĽM£®1,5£©£Ľ£®2£©2£ľm£ľ4£Ľ£®3£©P1£®![]() £©£¨P2£®
£©£¨P2£®![]() £©£¨P3£®3£¨1£©£¨P4£®©Ā3£¨7£©£ģ
£©£¨P3£®3£¨1£©£¨P4£®©Ā3£¨7£©£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©ĹęĶ„A°ĘĶ„CĶń◊ÝĪÍīķ»ŽļĮ żĹ‚őŲ Ĺ£¨ľīŅ…«ů≥Ųb°ĘcĶń÷Ķ£¨Õ®ĻżŇš∑Ĺ∑®Ķ√ĶĹĶ„MĶń◊ÝĪÍ£Ľ£®2£©Ķ„M «—ō◊Ň∂‘≥∆÷Š÷ĪŌŖx=1ŌÚŌ¬∆Ĺ“∆Ķń£¨Ņ…Ō»«ů≥Ų÷ĪŌŖACĶńĹ‚őŲ Ĺ£¨Ĺęx=1īķ»Ž«ů≥ŲĶ„M‘ŕŌÚŌ¬∆Ĺ“∆ Ī”ŽAC°ĘABŌŗĹĽ ĪyĶń÷Ķ£¨ľīŅ…Ķ√ĶĹmĶń»°÷Ķ∑∂őߣĽ£®3£©”…Ő‚“‚∑÷őŲŅ…Ķ√°ŌMCP=90°„£¨‘ڻ۰ųPCM”Ž°ųBCDŌŗň∆£¨‘Ú“™ĹÝ––∑÷ņŗŐ÷¬Ř£¨∑÷≥…°ųPCM°◊°ųBDCĽÚ°ųPCM°◊°ųCDBŃĹ÷÷£¨»ĽļůņŻ”√ĪŖĶń∂‘”¶Ī»÷Ķ«ů≥ŲĶ„◊ÝĪÍ£ģ
‘Ő‚Ĺ‚őŲ£ļ£®1£©į—Ķ„A£®3£¨1£©£¨Ķ„C£®0£¨4£©īķ»Ž∂ĢīőļĮ ży=©Āx2+bx+cĶ√£¨
![]() Ĺ‚Ķ√
Ĺ‚Ķ√![]() °ŗ∂ĢīőļĮ żĹ‚őŲ Ĺő™y=©Āx2+2x+4£¨ Ňš∑ĹĶ√y=©Ā£®x©Ā1£©2+5£¨
°ŗ∂ĢīőļĮ żĹ‚őŲ Ĺő™y=©Āx2+2x+4£¨ Ňš∑ĹĶ√y=©Ā£®x©Ā1£©2+5£¨
°ŗĶ„MĶń◊ÝĪÍő™£®1£¨5£©£Ľ
£®2£©…Ť÷ĪŌŖACĹ‚őŲ Ĺő™y=kx+b£¨į—Ķ„A£®3£¨1£©£¨C£®0£¨4£©īķ»ŽĶ√£¨![]() Ĺ‚Ķ√£ļ
Ĺ‚Ķ√£ļ![]()
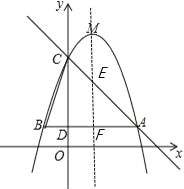
°ŗ÷ĪŌŖACĶńĹ‚őŲ Ĺő™y=©Āx+4£¨»ÁÕľňý ĺ£¨∂‘≥∆÷Š÷ĪŌŖx=1”Ž°ųABCŃĹĪŖ∑÷ĪūĹĽ”ŕĶ„E°ĘĶ„F
į—x=1īķ»Ž÷ĪŌŖACĹ‚őŲ Ĺy=©Āx+4Ĺ‚Ķ√y=3£¨‘ÚĶ„E◊ÝĪÍő™£®1£¨3£©£¨Ķ„F◊ÝĪÍő™£®1£¨1£©
°ŗ1£ľ5©Ām£ľ3£¨Ĺ‚Ķ√2£ľm£ľ4£Ľ
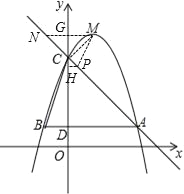
£®3£©Ń¨Ĺ”MC£¨◊ųMG°Õy÷Š≤Ę—”≥§ĹĽAC”ŕĶ„N£¨‘ÚĶ„G◊ÝĪÍő™£®0£¨5£© °ŖMG=1£¨GC=5©Ā4=1
°ŗMC=![]() =
=![]() £¨ į—y=5īķ»Žy=©Āx+4Ĺ‚Ķ√x=©Ā1£¨‘ÚĶ„N◊ÝĪÍő™£®©Ā1£¨5£©£¨
£¨ į—y=5īķ»Žy=©Āx+4Ĺ‚Ķ√x=©Ā1£¨‘ÚĶ„N◊ÝĪÍő™£®©Ā1£¨5£©£¨
°ŖNG=GC£¨GM=GC£¨ °ŗ°ŌNCG=°ŌGCM=45°„£¨ °ŗ°ŌNCM=90°„£¨
”…īňŅ…÷™£¨»ŰĶ„P‘ŕAC…Ō£¨‘Ú°ŌMCP=90°„£¨‘ÚĶ„D”ŽĶ„CĪōő™Ōŗň∆»żĹ«–ő∂‘”¶Ķ„
ĘŔ»Ű”–°ųPCM°◊°ųBDC£¨‘Ú”–![]()
°ŖBD=1£¨CD=3£¨ °ŗCP=![]() =
=![]() =
=![]() £¨ °ŖCD=DA=3£¨ °ŗ°ŌDCA=45°„£¨
£¨ °ŖCD=DA=3£¨ °ŗ°ŌDCA=45°„£¨
»ŰĶ„P‘ŕy÷Š”“≤ŗ£¨◊ųPH°Õy÷Š£¨ °Ŗ°ŌPCH=45°„£¨CP=![]() °ŗPH=
°ŗPH=![]() =
=![]()
į—x=![]() īķ»Žy=©Āx4£¨Ĺ‚Ķ√y=
īķ»Žy=©Āx4£¨Ĺ‚Ķ√y=![]() £¨ °ŗP1£®
£¨ °ŗP1£®![]() £©£Ľ
£©£Ľ
Õ¨ņŪŅ…Ķ√£¨»ŰĶ„P‘ŕy÷Š◊ů≤ŗ£¨‘Úį—x=©Ā![]() īķ»Žy=©Āx+4£¨Ĺ‚Ķ√y=
īķ»Žy=©Āx+4£¨Ĺ‚Ķ√y=![]() °ŗP2£®
°ŗP2£®![]() £©£Ľ
£©£Ľ
Ęŕ»Ű”–°ųPCM°◊°ųCDB£¨‘Ú”–![]() °ŗCP=
°ŗCP=![]() =3
=3![]() °ŗPH=3
°ŗPH=3![]() °¬
°¬![]() =3£¨
=3£¨
»ŰĶ„P‘ŕy÷Š”“≤ŗ£¨į—x=3īķ»Žy=©Āx+4£¨Ĺ‚Ķ√y=1£Ľ
»ŰĶ„P‘ŕy÷Š◊ů≤ŗ£¨į—x=©Ā3īķ»Žy=©Āx+4£¨Ĺ‚Ķ√y=7
°ŗP3£®3£¨1£©£ĽP4£®©Ā3£¨7£©£ģ
°ŗňý”–∑ŻļŌŐ‚“‚Ķ√Ķ„P◊ÝĪÍ”–4łŲ£¨∑÷Īūő™P1£®![]() £©£¨P2£®
£©£¨P2£®![]() £©£¨P3£®3£¨1£©£¨P4£®©Ā3£¨7£©£ģ
£©£¨P3£®3£¨1£©£¨P4£®©Ā3£¨7£©£ģ

 √Ż–£ŅőŐ√ŌĶŃ–īūįł
√Ż–£ŅőŐ√ŌĶŃ–īūįł