题目内容
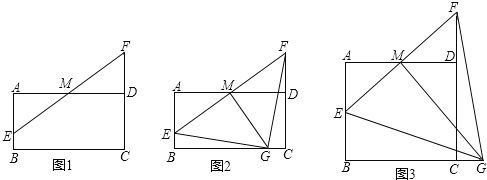
【题目】如图,AB为⊙O的直径,C,E为⊙O上的两点,AC平分∠EAB,CD⊥AE于D.
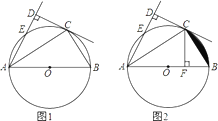
(1)求证:CD为⊙O的切线;
(2)过点C作CF⊥AB于F,如图2,判断CF和AF,DE之间的数量关系,并证明之;
(3)若AD-OA=1.5,AC=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)CF2=AFDE;(3)![]() .
.
【解析】
(1)连接OC,如图1,由AC平分∠EAB得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,则有AD⊥CD可判断OC⊥CD,然后根据切线的判定定理得到CD为⊙O的切线;
(2)连结CE,如图2,根据角平分线的性质得CD=CF,再证明Rt△ACD≌△ACF得到AD=AF,接着证明Rt△DEC∽Rt△DCA,理由相似得性质得DE:DC=DC:DA,然后利用等线段代换即可得到CF2=DEAF;
(3)设⊙O的半径为r,由AD=AF,AD-OA=1.5可得到OF=1.5,再证明Rt△ACF∽Rt△ABC,利用相似比可计算出r=3,接着在Rt△FCO中,利用余弦的定义可求出∠COB=60°,然后根据扇形的面积公式和等边三角形面积公式和S阴影部分=S扇形BOC-S△BOC进行计算即可.
(1)解:连接OC,如图1.
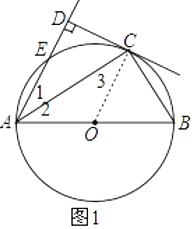
∵AC平分∠EAB,
∴∠1=∠2.
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD.
∵AD⊥CD,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)解:CF2=AFDE.理由如下:
连结CE,如图2.
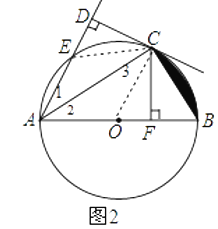
∵AC平分∠EAB,CD⊥AE,CF⊥AB,
∴CD=CF.
在Rt△ACD和△ACF中,![]() ,
,
∴Rt△ACD≌△ACF,
∴AD=AF.
∵四边形CEAB内接于⊙O,
∴∠DEC=∠B.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠2=90°,∠1+∠ACD=90°,∠1=∠2,
∴∠DEC=∠ACD,
∴Rt△DEC∽Rt△DCA,
∴DE:DC=DC:DA,
∴DC2=DEDA,
∴CF2=DEAF;
(3)解:设⊙O的半径为r.
∵AD=AF,而AD﹣OA=1.5,
∴AF=AD=OA+OF=r+1.5,∴OF=1.5.
∵∠CAB=∠FAC,
∴Rt△ACF∽Rt△ABC,
∴ ![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:r=3或r=-![]() (舍去).
(舍去).
在Rt△FCO中,∵cos∠COF=![]() =
=![]() =
=![]() ,
,
∴∠COB=60°,
∴S阴影部分=S扇形BOC﹣S△BOC
=![]() -
-![]() ×32=
×32=![]() π-
π-![]() .
.
故答案为:(1)证明见解析;(2)CF2=AFDE;(3)![]() .
.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案【题目】某射击教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”、“变小”或“不变”)