题目内容
如图：在梯形ABCD中，AD//BC,AD=2，AC=4，BC=6，BD=8，求梯形ABCD的面积。
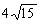
过点D做DE//AC交BC的延长线于点E,
∵AD//BC
∴AD=CE,S△ABD= S△DCE
∴S梯形ABCD= S△BDE
∵AD=2，AC=4，BC=6，BD=8
∴DE=AC=4，BE=BC+CE=6+2=8
∴BE=BD=8
即△BDE是等腰三角形.
过点B做BF⊥DE于F,
由勾股定理得BF=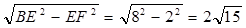
∴S梯形ABCD= S△BDE=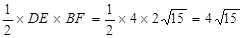
∵AD//BC
∴AD=CE,S△ABD= S△DCE
∴S梯形ABCD= S△BDE
∵AD=2，AC=4，BC=6，BD=8
∴DE=AC=4，BE=BC+CE=6+2=8
∴BE=BD=8
即△BDE是等腰三角形.
过点B做BF⊥DE于F,
由勾股定理得BF=
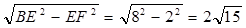
∴S梯形ABCD= S△BDE=
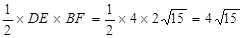
练习册系列答案
阅读快车系列答案
相关题目
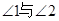满足 关系时AB//CD，(只要写出一个你认为成立的条件)。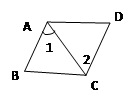
按如图的方式折叠，得到菱形
，若
，则
的长为（ ）
中，
两点在边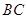
上，且四边形
是平行四边形．
与
时，求证：
是矩形．