题目内容
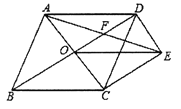
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() 将
将![]() 绕点
绕点![]() .按顺时针方向旋转
.按顺时针方向旋转![]() 得
得![]() , 连接
, 连接![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时, 试判断
时, 试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

【答案】(1)见解析;(2)![]() 是直角三角形,理由见解析;(3)当
是直角三角形,理由见解析;(3)当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
【解析】
(1)根据旋转的性质得到![]() ,再根据旋转角的度数得到∠OCD的度数,根据等边三角形的判定方法,即可证明.
,再根据旋转角的度数得到∠OCD的度数,根据等边三角形的判定方法,即可证明.
(2)根据旋转前后对应的两个三角形全等可得△BOC≌△ADC,利用全等三角形的性质得到∠ADC=∠BOC=![]() ,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,再结合周角为360°,求出∠AOD的度数,探究是否存在等腰直角三角形的情况,进而判断△AOD的形状;
,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,再结合周角为360°,求出∠AOD的度数,探究是否存在等腰直角三角形的情况,进而判断△AOD的形状;
(3)需要分三种情况讨论,即①要使AO=AD,需∠AOD=∠ADO;②要使OA=OD,需∠OAD=∠ADO;③要使OD=AD,需∠OAD=∠AOD;如对于①,∠AOD=190°-![]() ,∠ADO=
,∠ADO=![]() -60°,再结合∠AOD=∠ADO建立
-60°,再结合∠AOD=∠ADO建立![]() 的方程,求出
的方程,求出![]() 的度数,同理可以计算其他两种情况.
的度数,同理可以计算其他两种情况.
(1)证明:由旋转的性质得:![]() ,
,
![]()
![]() 是等边三角形;
是等边三角形;
(2)当![]() ,即
,即![]() °时,
°时,
![]() 是直角三角形.理由如下:
是直角三角形.理由如下:
由旋转的性质得:![]()
![]()
又是![]() 等边三角形,
等边三角形,
![]()
![]()
即![]() 是直角三角形;
是直角三角形;
(3)分三种情况:
①![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]() ;
;
②![]() 时,
时,![]()
![]()
![]()
![]()
![]() ;
;
③![]() 时,
时,![]()
![]()
![]() .
.
综上所述:当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目