��Ŀ����
����Ŀ����ͼ��ʾ��A��B�������50ǧ�ף�����ij������1ʱ�����г���A�س���ʻ��B�أ���Ҳ��ͬ��������Ħ�г�����ͬ·�ߴ�A�س���ʻ��B�أ���ͼ��ʾ��ͼ�е�����PQR���߶�MN�ֱ��ʾ�ס�������ʻ��·��S��ʱ��t�Ĺ�ϵ.��ش��������⣺
(1)������һ�������ĸ���?������ʱ��?
(2)������һ���絽��B��?��ʱ��?
(3)����Ħ�г����ٶȺͼ������г���ȫ�̵�ƽ���ٶȷֱ��Ƕ���?
(4)�������ͼ���ϵ����ݣ�����ҳ�����ʱ���ϼ�?
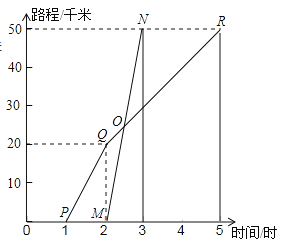
���𰸡���1������,�����1 h;��2���Ҹ���,�絽2 h;��3����ƽ���ٶ�12.5km/h, �ҵ�ƽ���ٶ���50km/h;(4) �ҳ���0.5 h���ϼ�
��������
��1����2����ͼ��֪��
��3����ͼ�е����������ߵ�·�̶���50ǧ������һ������4Сʱ����һ������1Сʱ�������ٶ�=![]() ���������ó���
����������
��4����ͼ�е�����������ȫ��ʱ��ǰ1Сʱ�ٶ�Ϊ20ǧ��/Сʱ���ӵ�2Сʱ��ʼ���ٶ�Ϊ![]() =10ǧ��/Сʱ��������ҳ���xСʱ���ϼ������ͼ�п������ڼ��ٶ�Ϊ10ǧ��/Сʱʱ�������������Լ�·��Ϊ20+10x���ҵ�·��Ϊ50x���з��̽�����ɣ�
=10ǧ��/Сʱ��������ҳ���xСʱ���ϼ������ͼ�п������ڼ��ٶ�Ϊ10ǧ��/Сʱʱ�������������Լ�·��Ϊ20+10x���ҵ�·��Ϊ50x���з��̽�����ɣ�
��1��������1ʱ������������2ʱ���������Լ����������1Сʱ��
��2����5ʱ��������3ʱ�����������Ҹ������絽2Сʱ��
��3���ҵ��ٶ�=![]() =50��ǧ��/ʱ������ƽ���ٶ�=
=50��ǧ��/ʱ������ƽ���ٶ�=![]() =12.5��ǧ��/ʱ����
=12.5��ǧ��/ʱ����
��4�����ҳ���xСʱ���ϼ��������������50x=20+10x��x=0.5��
�����ҳ���0.5Сʱ���ϼף�

����Ŀ��ij������ӵ���һ��ѡ��һ����Ա.�������������������ͬѧ����5��3����Ͷ������,ÿ��ÿ��Ͷ10����,ͼ��¼����������ͬѧ5��Ͷ����Ͷ�еĸ���.

(1)�������ͼ�е�����,��д�±�;
���� | ƽ���� | ���� | ���� |
���� | 7 | ||
��� | 7 | 2.8 |
(2)����Ϊ˭�ijɼ��Ƚ��ȶ�,Ϊʲô?
(3)�����ǽ���,�����ѡ˭?��Ҫ˵������.