��Ŀ����
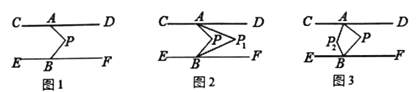
����Ŀ����ͼ1,��ֱ֪��CD//EF ,��A��B�ֱ���ֱ��CD��EF�ϡ�PΪ��ƽ����һ��
(1)����DAP= 40�� , ��FBP=70��,���APB�Ķ����Ƕ���?
(2)ֱ��д����DAP, ��FBP, ��APB֮����ʲô��ϵ?
(3)����(2)�Ľ��۽��
����ͼ2, AP1��BP1,�ֱ�ƽ�֡�DAP,��FBP,����д����P���P1,��������ϵ����˵�����ɣ�
����ͼ3, AP2�� BP2�ֱ�ƽ�֡�CAP,��EBP,����APB=��,���AP2B (�ú��µĴ���ʽ��ʾ).
���𰸡���1����APB=110�㣻��2����APB=��DAP+��FBP����3���١�P=2��P1����180��-0.5����
��������
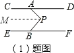
��1����P����PM��CD������ƽ���ߵ����ʼ�����⣻
��2���ɣ�1������д����ϵ��
��3���ٸ��ݽ�ƽ���ߵ����ʼ�ƽ���ߵ����ʼ�����⣻�ڸ������Ĺ��ɵõ���APB=��DAP+��FBP����AP2B=��CAP2+��EBP2��Ȼ����ݽ�ƽ���ߵ����ʼ�ƽ�ǵļ�����ʽ���.
��1����P����PM��CD��
���DAP=��APM=40�� ,
��CD//EF����PM��EF
���MPB=��FBP=70��,
���APB=110��
��2���ɣ�1����֪��DAP, ��FBP, ��APB֮��Ĺ�ϵΪ��APB=��DAP+��FBP��
��3���١�P=2��P1��
�ɣ�2������P=��DAP+��FBP��
�֡�AP1B=��DAP1+��FBP1=![]() ��DAP+
��DAP+![]() ��FBP=
��FBP=![]() (��DAP+��FBP)=
(��DAP+��FBP)=![]() ��P
��P
����P=2��P1
���ɣ�2���á�APB=��DAP+��FBP����AP2B=��CAP2+��EBP2��
��AP2�� BP2�ֱ�ƽ�֡�CAP,��EBP,
���CAP2=![]() ��CAP����EBP2=
��CAP����EBP2=![]() ��EBP
��EBP
���AP2B=![]() ��CAP +
��CAP +![]() ��EBP
��EBP
=![]() ��180��-��DAP��+
��180��-��DAP��+![]() ��180��-��FBP��
��180��-��FBP��
=180��-![]() ����DAP+��FBP��
����DAP+��FBP��
=180��-0.5��

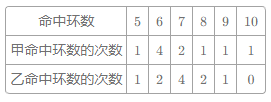
����Ŀ��ij������ӵ���һ��ѡ��һ����Ա.�������������������ͬѧ����5��3����Ͷ������,ÿ��ÿ��Ͷ10����,ͼ��¼����������ͬѧ5��Ͷ����Ͷ�еĸ���.

(1)�������ͼ�е�����,��д�±�;
���� | ƽ���� | ���� | ���� |
���� | 7 | ||
��� | 7 | 2.8 |
(2)����Ϊ˭�ijɼ��Ƚ��ȶ�,Ϊʲô?
(3)�����ǽ���,�����ѡ˭?��Ҫ˵������.