题目内容
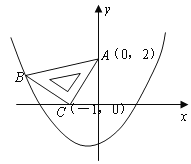
【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2![]() 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.

A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
【答案】C
【解析】解:①连接AC,交BD于点O,∵四边形ABCD是菱形,∴AB=BC,BD⊥AC,AO=BO
∴点A,点C关于直线BD对称,∴M点与O点重合时AM+CM的值最小为AC的值
∵∠ABC=60,∴△ABC是等边三角形,∴AB=AC,∵AB=1,∴AC=1,即AM+CM的值最小为1,故①正确.
②∵△ABE是等边三角形,∴BA=BE,∠ABE=60°.
∵∠MBN=60°,∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,∴△AMB≌△ENB(SAS),故②正确.
③∵S△ABE+S△ABM=S四边形AMBE
S△ACD+S△AMC=S四边形ADCM,且S△AMB≠S△AMC,∴S△ABE+S△ABM≠S△ACD+S△AMC,∴S四边形AMBE≠S四边形ADCM,故③错误.
④假设AN⊥BE,且AE=AB,∴AN是BE的垂直平分线,∴EN=BN=BM=MN,∴M点与O点重合,∵条件没有确定M点与O点重合,故④错误.
⑤如图,连接MN,由(1)知,△AMB≌△ENB,∴AM=EN,∵∠MBN=60°,MB=NB,∴△BMN是等边三角形,∴BM=MN,∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
过E点作EF⊥BC交CB的延长线于F,∴∠EBF=180°﹣120°=60°,设菱形的边长为x,∴BF=![]() x,EF=
x,EF=![]() x,在Rt△EFC中,∵EF2+FC2=EC2,∴
x,在Rt△EFC中,∵EF2+FC2=EC2,∴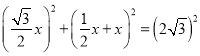 ,解得x=2,故⑤正确.
,解得x=2,故⑤正确.
综上所述,正确的答案是:①②⑤,故选C.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/ | -20 | -10 | 0 | 10 | 20 | 30 |
声速/( | 318 | 324 | 330 | 336 | 342 | 348 |
下列说法中错误的是( )
A.在这个变化过程中,当温度为10![]() 时,声速是336
时,声速是336![]()
B.温度越高,声速越快
C.当空气温度为20![]() 时,声音5
时,声音5![]() 可以传播1740
可以传播1740![]()
D.当温度每升高10![]() ,声速增加6
,声速增加6![]()