Question

【题目】阅读下列材料，完成下列各题：平面内的两条直线有相交和平行两种位置关系。

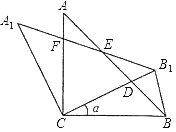
（1）如图1，若，点P在AB，CD之间，求证：∠BPD=∠B+∠D；

（2）在图1中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图2，请写出，∠B，，之间的数量关系并说明理由；

（3）利用（2）的结论，求图3中+∠G=n×90°，则n=____.

Answer 1

【答案】（1）见解析（2）∠BPD=∠B+∠D+∠BQD（3）6

【解析】

（1）作PQ∥AB，根据平行线性质得AB∥PQ∥CD，则∠1=∠B，∠2=∠D，所以∠BPD=∠B+∠D；

（2）连结QP并延长到E，根据三角形外角性质得∠1=∠B+∠BQP，∠2=∠D+∠DQP，然后把两式相加即可得到∠BPD=∠B+∠D+∠BQD；

（3）连结AG，根据三角形内角和定理和对顶角相等得到∠B+∠F=∠BGA+∠FAG，则可把∠A+∠B+∠C+∠D+∠E+∠F+∠G化为五边形ACDEG的内角和，然后根据多边形的内角和定理求解．

（1）证明：∠BPD=∠B+∠D．

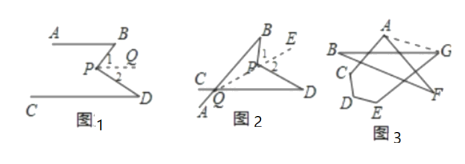
作PQ∥AB，如图1，

∵AB∥CD，

∴AB∥PQ∥CD，

∴∠1=∠B，∠2=∠D，

∴∠BPD=∠B+∠D；

（2）∠BPD=∠B+∠D+∠BQD．理由如下：

连结QP并延长到E，如图2，

∵∠1=∠B+∠BQP，∠2=∠D+∠DQP，

∴∠1+∠2=∠B+∠BQP+∠D+∠DQP，

∴∠BPD=∠B+∠D+∠BQD；

（3）连结AG，如图3，

∵∠B+∠F=∠BGA+∠FAG，

∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠FAG+∠C+∠D+∠E+∠BAG+∠G=（5-2）×180°=6×90°，

∴n=6．

故答案为6．