ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ГЩе§БШР§ЃЌ
ГЩе§БШР§ЃЌ ![]() гы
гы![]() ГЩЗДБШР§ЃЌВЂЧвЕБ
ГЩЗДБШР§ЃЌВЂЧвЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓ
ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ![]() ЃЉЕБ
ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ![]() ЃЉ
ЃЉ![]() ЃЛЃЈ
ЃЛЃЈ![]() ЃЉ
ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЪзЯШИљОн![]() гыxГЩе§БШР§ЃЌ
гыxГЩе§БШР§ЃЌ ![]() гыxГЩЗДБШР§ЃЌЧвЕБx=1ЪБЃЌy=4ЃЛЕБx=2ЪБЃЌy=5ЃЌЧѓГі
гыxГЩЗДБШР§ЃЌЧвЕБx=1ЪБЃЌy=4ЃЛЕБx=2ЪБЃЌy=5ЃЌЧѓГі![]() КЭ
КЭ![]() гыxЕФЙиЯЕЪНЃЌНјЖјЧѓГіyгыxЕФЙиЯЕЪНЃЌЃЈ2ЃЉИљОнЃЈ1ЃЉЮЪЧѓГіЕФyгыxжЎМфЕФЙиЯЕЪНЃЌСюy=0ЃЌМДПЩЧѓГіxЕФжЕЃЎ
гыxЕФЙиЯЕЪНЃЌНјЖјЧѓГіyгыxЕФЙиЯЕЪНЃЌЃЈ2ЃЉИљОнЃЈ1ЃЉЮЪЧѓГіЕФyгыxжЎМфЕФЙиЯЕЪНЃЌСюy=0ЃЌМДПЩЧѓГіxЕФжЕЃЎ
БОЬтНтЮіЃК
ЃЈ![]() ЃЉЩш
ЃЉЩш![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
ЁпЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ
Ёр
НтЕУЃЌ ![]() ЃЌ
ЃЌ
Ёр![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉАб
ЃЉАб![]() ДњШы
ДњШы![]() ЕУЃЌ
ЕУЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЕуОІЃКБОЬтПМВщСЫгУД§ЖЈЯЕЪ§ЗЈЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃКЃЈ1ЃЉЩшГіКЌгаД§ЖЈЯЕЪ§ЕФЗДБШР§КЏЪ§НтЮіЪНy=kx(kЮЊГЃЪ§ЃЌkЁй0);(2)АбвбжЊЬѕМўЃЈздБфСПгыЖдгІжЕЃЉДњШыНтЮіЪНЃЌЕУЕНД§ЖЈЯЕЪ§ЕФЗНГЬЃЛЃЈ3ЃЉНтЗНГЬЃЌЧѓГіД§ЖЈЯЕЪ§ЃЛЃЈ4ЃЉаДГіНтЮіЪН.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() Чв
Чв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
(1)ЧѓжЄ:![]() ;
;
(2)ШєСтаЮ![]() ЕФБпГЄЮЊ2,
ЕФБпГЄЮЊ2, ![]() .Чѓ
.Чѓ![]() ЕФГЄ.
ЕФГЄ.
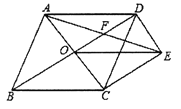
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌдйИљОнСтаЮЕФЖдНЧЯпЛЅЯрДЙжБЧѓГіЁЯCOD=90ЁуЃЌжЄУїOCEDЪЧОиаЮЃЌПЩЕУOE=CDМДПЩЃЛ
ЃЈ2ЃЉИљОнСтаЮЕФаджЪЕУГіAC=ABЃЌдйИљОнЙДЙЩЖЈРэЕУГіAEЕФГЄЖШМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКдкСтаЮABCDжаЃЌOC=![]() ACЃЎ
ACЃЎ
ЁрDE=OCЃЎ
ЁпDEЁЮACЃЌ
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЎ
ЁпACЁЭBDЃЌ
ЁрЦНааЫФБпаЮOCEDЪЧОиаЮЃЎ
ЁрOE=CDЃЎ
ЃЈ2ЃЉдкСтаЮABCDжаЃЌЁЯABC=60ЁуЃЌ
ЁрAC=AB=2ЃЎ
ЁрдкОиаЮOCEDжаЃЌ
CE=OD=![]() ЃЎ
ЃЎ
дкRtЁїACEжаЃЌ
AE=![]() ЃЎ
ЃЎ




