题目内容
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.
【答案】
(1)证明:∵E是△ABC的内心,
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE
(2)证明:连接CD.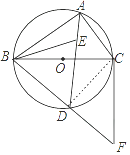
∵DA平分∠BAC,
∴∠DAB=∠DAC,
∴ ![]() =
= ![]() ,
,
∴BD=CD,
∵BD=DF,
∴CD=DB=DF,
∴∠BCF=90°,
∴BC⊥CF,
∴CF是⊙O的切线
【解析】(1)三角形的三内角平分线交于一点。该点叫做三角形的内心。根据三角形的内心的定义可得∠BAE=∠CAE,∠EBA=∠EBC,再根据三角形的一个外角等于和它不相邻的两个内角的和可得∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,结合已知条件可证得∠DBE=∠DEB,由等角对等边可得DB=DE。
(2)连接CD,要证CF是⊙O的切线,只须证∠BCF=90°,根据已知条件DA平分∠BAC可证BD=CD,结合已知BD=DF可得CD=DB=DF,则∠BCF=90°,结论可得。

 考前必练系列答案
考前必练系列答案【题目】已知函数![]() ,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是
,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
请你根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行探究.
之间的变化规律,对该函数的图象与性质进行探究.
(1)如图,在平面直角坐标系![]() 中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;

(2)请根据图象写出该函数的一条性质: .
(3)当![]() 时,
时,![]() 的取值范围为 ,则
的取值范围为 ,则![]() 的取值范围为 .
的取值范围为 .






