Question

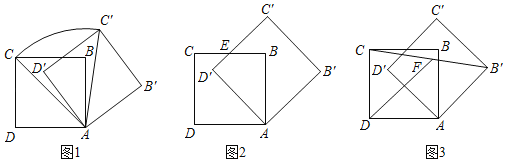
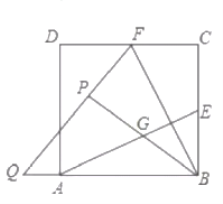
【题目】如图，在正方形中，分别为的中点，连接交于点，将沿对折，得到，延长交延长于点若则的值为（ ）

A.1B.2C.3D.

Answer 1

【答案】D

【解析】

先根据折叠的性质得到△BCF≌△BPF，Rt△ABM≌Rt△BMP，在Rt△DMF中，MF2＝FD2＋DM2,列式求出AM，再根据相似三角形求出AQ，得到BQ的长，再根据勾股定理求出AE的长，代入即可求解．

如图，连接BM，

在正方形中，分别为的中点，

∵折叠，

∴△BCF≌△BPF

∴BC＝BP，∠CBF＝∠PBF,CF=PF=DF=

∴AB＝BP=且BM＝BM

∴Rt△ABM≌Rt△BMP

∵在Rt△DMF中，MF2＝FD2＋DM2．

∴（＋AM）2＝（）2+（AM）2

∴AM＝，

∴DM＝-=，

∵DF∥AQ

∴△DFM∽△AQM

∴

即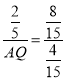

解得AQ=

∴BQ=AQ+AB=+=1

∵E点是AE的中点，

∴BE=,

则AE=

∴=

∴=1+=

故选D．