题目内容
【题目】若边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,记旋转角为a.
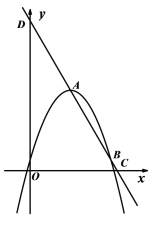
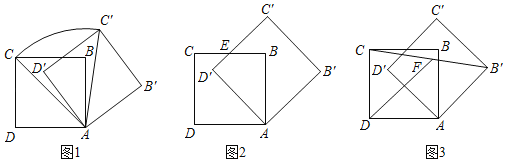
(I)如图1,当a=60°时,求点C经过的弧![]() 的长度和线段AC扫过的扇形面积;
的长度和线段AC扫过的扇形面积;
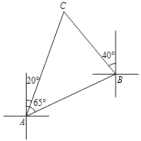
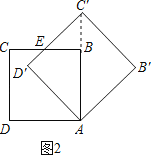
(Ⅱ)如图2,当a=45°时,BC与D′C′的交点为E,求线段D′E的长度;
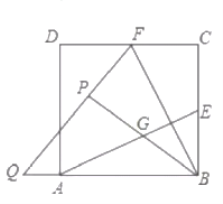
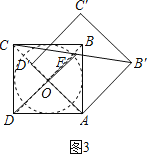
(Ⅲ)如图3,在旋转过程中,若F为线段CB′的中点,求线段DF长度的取值范围.
【答案】(I)12π;(Ⅱ)D′E=6![]() ﹣6;(Ⅲ)3
﹣6;(Ⅲ)3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.
【解析】
(Ⅰ)根据正方形的性质得到AD=CD=6,∠D=90°,由勾股定理得到AC=6![]() ,根据弧长的计算公式和扇形的面积公式即可得到结论;
,根据弧长的计算公式和扇形的面积公式即可得到结论;
(Ⅱ)连接BC′,根据题意得到B在对角线AC′上,根据勾股定理得到AC′=![]() =6
=6![]() ,求得BC′=6
,求得BC′=6![]() ﹣6,推出△BC′E是等腰直角三角形,得到C′E=
﹣6,推出△BC′E是等腰直角三角形,得到C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,于是得到结论;
,于是得到结论;
(Ⅲ)如图3,连接DB,AC相交于点O,则O是DB的中点,根据三角形中位线定理得到FO=![]() AB′=3,推出F在以O为圆心,3为半径的圆上运动,于是得到结论.
AB′=3,推出F在以O为圆心,3为半径的圆上运动,于是得到结论.
解:(Ⅰ)∵四边形ABCD是正方形,
∴AD=CD=6,∠D=90°,
∴AC=6![]() ,
,
∵边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,
∴∠CAC′=60°,
∴![]() 的长度=
的长度=![]() =2
=2![]() π,线段AC扫过的扇形面积=
π,线段AC扫过的扇形面积=![]() =12π;
=12π;
(Ⅱ)解:如图2,连接BC′,
∵旋转角∠BAB′=45°,∠BAD′=45°,
∴B在对角线AC′上,
∵B′C′=AB′=6,
在Rt△AB′C′中,AC′=![]() =6
=6![]() ,
,
∴BC′=6![]() ﹣6,
﹣6,
∵∠C′BE=180°﹣∠ABC=90°,∠BC′E=90°﹣45°=45°,
∴△BC′E是等腰直角三角形,
∴C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,
,
∴D′E=C′D′﹣EC′=6﹣(12﹣6![]() )=6
)=6![]() ﹣6;
﹣6;
(Ⅲ)如图3,连接DB,AC相交于点O,
则O是DB的中点,
∵F为线段BC′的中点,
∴FO=![]() AB′=3,
AB′=3,
∴F在以O为圆心,3为半径的圆上运动,
∵DO=3![]() ,
,
∴DF最大值为3![]() +3,DF的最小值为3
+3,DF的最小值为3![]() ﹣3,
﹣3,
∴DF长的取值范围为3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.

【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.