题目内容

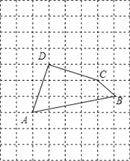
【题目】如图，将四边形ABCD放在每个小正方形的边长为1的网格中，点A．B、C、D均落在格点上．

（Ⅰ）计算AD2+DC2+CB2的值等于_____；

（Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AD2+DC2+CB2，并简要说明画图方法（不要求证明）．

【答案】22

【解析】

（1）直接根据勾股定理分别计算的值，再相加即可；
（2）以AB为边做正方形，这个正方形的面积是26，再作同底边平行四边形，使它的面积为4，直线MN交AH于点Q，交GB于点P，得矩形ABPQ；

解：(1)∵

∴

故答案为22；

(2)如图，以AB为边做正方形ABGH，再作平行四边形HMNG，直线MN交AH于点Q，交GB于点P，矩形ABPQ即为所求．

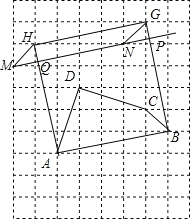
理由是：∵

∴S矩形HQNG=SHMNG=4，

∵S正方形ABGH=

∴S矩形ABPQ=264=22，

所以画出的矩形ABPQ的面积等于

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠ACB＝90°，点D是AB边上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．

（1）求证：BD＝BF；

（2）填空：

①若⊙O的半径为5，tanB＝，则CF＝　 　；

②若⊙O与BF相交于点H，当∠B的度数为　 　时，四边形OBHE为菱形．

【题目】如图，在Rt△ABC中，∠ABC=90°，AB=4，BC=3，以点B为圆心，适当长为半径画弧交边于D，E两点（按照A，D，E，C依次排列，且D、E不重合）.过D、E分别作AB和BC的垂线段交于F、G两点，如果线段DF=x，EG=y，则x、y的关系式为（ ）

A.20x-15y=B.20x-15y=

C.15x-20y=D.15x-20y=

【题目】已知抛物线y=的图像与轴的一个交点为A（-1，0），另一个交点为B，与轴交于点C（0，﹣3），顶点为D．

（1）求二次函数的解析式和点D的坐标；

（2）若点M是抛物线在轴下方图像上的一动点，过点M作MN∥轴交线段BC于点N，当MN取最大值时，点M 的坐标；

（3）将该抛物线向上或向下平移，使得新抛物线的顶点D落在x轴上，原抛物线上一点P平移后的对应点为Q，如果∠OQP=∠OPQ，试求点Q的坐标．

【题目】已知：点M是平行四边形ABCD对角线AC所在直线上的一个动点（点M不与点A、C重合），分别过点A、C向直线BM作垂线，垂足分别为点E、F，点O为AC的中点．

⑴如图1,当点M与点O重合时，OE与OF的数量关系是 ．

⑵直线BM绕点B逆时针方向旋转，且∠OFE=30°．

①如图2，当点M在线段AC上时，猜想线段CF、AE、OE之间有怎样的数量关系？请你写出来并加以证明；

②如图3，当点M在线段AC的延长线上时，请直接写出线段CF、AE、OE之间的数量关系．

【题目】如图，抛物线经过，，三点．

（1）求抛物线的解析式；

（2）在抛物线的对称轴上有一点，使的值最小，求点的坐标；

（3）点为轴上一动点，在抛物线上是否存在一点，使以，，，四点构成的四边形为平行四边形？若存在，求点的坐标；若不存在，请说明理由．

【题目】如图，在平面直角坐标系中，，将绕点顺时针旋转，使点落在点处，得到，过点作平行于轴的直线交于点，交轴于点，直线交于点.，.

（1）求经过点、的反比例函数和直线：的解析式；

（2）过点作轴，求五边形的面积；

（3）直接写出当时的值．

【题目】如图，正方形和正方形中，点在上，，，是的中点，与交于点0．则的长为__________．

【题目】如图，已知中，，，，点，分别是边，上的动点，且，点关于的对称点恰好落在的内角平分线上，则长为_______________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网