题目内容
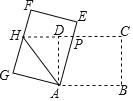
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
A. 15 B. 18 C. 20 D. 24
【答案】C
【解析】
连结AC,先由△AGH≌△ADH得到∠GHA=∠AHD,进而得到∠AHD=∠HAP,所以△AHP是等腰三角形,所以PH=PA=PC,所以∠HAC是直角,再在Rt△ABC中由勾股定理求出AC的长,然后由△HAC∽△ADC,根据![]() =
=![]() 求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
∵P是CH的中点,PH=PC,∵AH=AH,AG=AD,且AGH与ADH都是直角,∴△AGH≌△ADH,∴∠GHA=∠AHD,又∵GHA=HAP,∴∠AHD=∠HAP,∴△AHP是等腰三角形,∴PH=PA=PC,∴∠HAC是直角,在Rt△ABC中,AC=![]() =10,∵△HAC∽△ADC,∴
=10,∵△HAC∽△ADC,∴![]() =
=![]() ,∴AH=
,∴AH=![]() =
=![]() =7.5,又∵△HAC∽△HAD,
=7.5,又∵△HAC∽△HAD,![]() =
=![]() ,∴DH=4.5,∴HP=
,∴DH=4.5,∴HP=![]() =6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.
=6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某校团委组织“阳光助残”献爱心捐款活动,九年级(2)班学生捐款如表:
捐款金额(元) | 5 | 10 | 15 | 20 |
人数(人) | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是( )
A. 10元,15元 B. 15元,15元 C. 10元,20元 D. 16元,17元