Question

【题目】在△ABC中，AB＝AC＝5，BC＝8，点M是△ABC的中线AD上一点，以M为圆心作⊙M．设半径为r

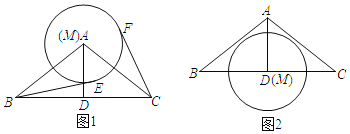
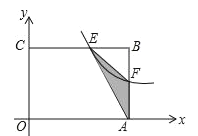
（1）如图1，当点M与点A重合时，分别过点B，C作⊙M的切线，切点为E，F．求证：BE＝CF；

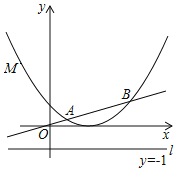
（2）如图2，若点M与点D重合，且半圆M恰好落在△ABC的内部，求r的取值范围；

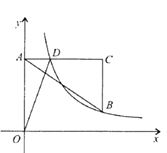
（3）当M为△ABC的内心时，求AM的长．

Answer 1

【答案】（1）见解析；（2）；（3）AM＝．

【解析】

（1）连接AE，AF，利用“HL”证Rt△BAE≌Rt△ACF即可得；

（2）作DG⊥AB，由AB＝AC＝5，AD是中线知AD⊥BC且AD＝＝3，依据BD×AD＝AB×DG可得DG＝，从而得出答案；

（3）作MH⊥AB，MP⊥AC，有MH＝MP＝MD，连接BM、CM，根据ABMH+BCMD+ACMP＝ADBC求出圆M的半径，从而得出答案．

解：（1）如图1，连接AE，AF，

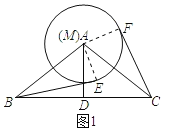
∵BE和CF分别是⊙O的切线，

∴∠BEA＝∠CFA＝90°，

∵AB＝AC，AE＝AF，

∴Rt△BAE≌Rt△ACF（HL），

∴BE＝CF；

（2）如图2，过点D作DG⊥AB于点G，

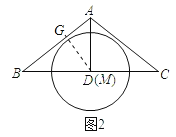
∵AB＝AC＝5，AD是中线，

∴AD⊥BC，

∴AD＝＝3，

∴BD×AD＝AB×DG，

∴DG＝，

∴当0＜r＜时，半圆M恰好落在△ABC内部；

（3）当M为△ABC的内心时，

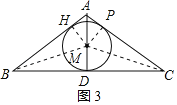
如图3，过M作MH⊥AB于H，作MP⊥AC于P，

则有MH＝MP＝MD，

连接BM、CM，

∴ABMH+BCMD+ACMP＝ADBC，

∴r＝，

∴AM＝AD﹣DM＝．