题目内容
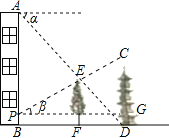
【题目】如图,在一居民楼AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为38°.从距离楼底B点2米的P处经过树顶E点恰好看到塔的顶部C点,且仰角β为28°.已知树高EF=8米,求塔CD的高度.(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
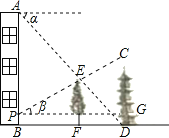
【答案】CD=13(米).
【解析】
根据题意求出∠EDF=38°,通过解直角△EFD求得FD,在Rt△PEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△PCG中,继而可求出CG的长度.
解:由题意知,∠EDF=α=38°,
∴FD=![]() =10(米).EH=8﹣2=6(米)
=10(米).EH=8﹣2=6(米)
在Rt△PEH中,∵![]() .
.
∴![]() .
.
∴BF=12(米)
PG=BD=BF+FD=12+10=22(米).
在直角△PCG中,∵![]() .
.
∴CG=PGtanβ≈22×0.5=11(米).
∴CD=11+2=13(米).

练习册系列答案
相关题目