题目内容
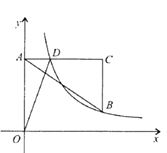
【题目】如图,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 轴,点
轴,点![]() 、
、![]() 的横坐标都是3,且
的横坐标都是3,且![]() ,点
,点![]() 在
在![]() 上,若反比例函数
上,若反比例函数![]() 的图象经过点
的图象经过点![]() 、
、![]() ,且
,且![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)将![]() 沿着
沿着![]() 折叠,设顶点
折叠,设顶点![]() 的对称点
的对称点![]() 的坐标是
的坐标是![]() ,求代数式
,求代数式![]() 的值.
的值.
【答案】(1)k=3;D(1,3);(2)m+3n=9
【解析】
(1)先根据![]() ,BC=2得出OA的长,再根据点B、C的横坐标都是3可知BC∥AO,故可得出B点坐标,再根据点B在反比例函数
,BC=2得出OA的长,再根据点B、C的横坐标都是3可知BC∥AO,故可得出B点坐标,再根据点B在反比例函数![]() 的图象上可求出k的值,由AC∥x轴可设点D(t,3)代入反比例函数的解析式即可得出t的值,进而得出D点坐标;
的图象上可求出k的值,由AC∥x轴可设点D(t,3)代入反比例函数的解析式即可得出t的值,进而得出D点坐标;
(2)过点A′作EF∥OA交AC于E,交x轴于F,连接OA′,根据AC∥x轴可知∠A′ED=∠A′FO=90°,由相似三角形的判定定理得出△DEA′∽△A′FO,设A′(m,n),可得出![]() ,再根据勾股定理可得出m2+n2=9,两式联立可得出
,再根据勾股定理可得出m2+n2=9,两式联立可得出![]() 的值.
的值.
解:(1)∵![]() ,BC=2,
,BC=2,
∴OA=3,
∵点B、C的横坐标都是3,
∴BC∥AO,
∴B(3,1),
∵点B在反比例函数![]() 的图象上,
的图象上,
∴![]() ,解得k=3,
,解得k=3,
∵AC∥x轴,
∴设点D(t,3),
∴3t=3,解得t=1,
∴D(1,3);
(2)过点A′作EF∥OA交AC于E,交x轴于F,连接OA′(如图所示),
∵AC∥x轴,
∴∠A′ED=∠A′FO=90°,
∵∠OA′D=90°,
∴∠A′DE=∠OA′F,
∴△DEA′∽△A′FO,
设A′(m,n),
∴![]() ,
,
又∵在Rt△A′FO中,m2+n2=9,
∴m+3n=9.


练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目