Question

【题目】如图①所示，直线L：y＝kx+5k与x轴负半轴、y轴正半轴分别交于A、B两点．

(1)当OA＝OB时，试确定直线L解析式；

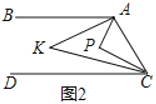
(2)在(1)的条件下，如图②所示，设Q为AB延长线上一点，连接OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若BN＝3，求MN的长；

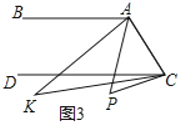
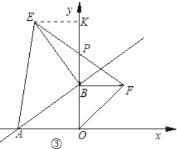
(3)当K取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边在第一、第二象限作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，问当点B在y轴上运动时，试猜想△ABP的面积是否改变，若不改变，请求出其值；若改变，请说明理由．

(4)当K取不同的值时，点B在y轴正半轴上运动，以AB为边在第二象限作等腰直角△ABE，则动点E在直线______上运动．(直接写出直线的表达式)

Answer 1

【答案】(1)y＝x+5；(2)MN＝7；(3)S△ABP＝；(4)y＝﹣x+5．

【解析】

（1）由直线L解析式，求出A与B坐标，根据OA=OB，求出m的值，即可确定出直线L解析式；
（2）由OA=OB，对顶角相等，且一对直角相等，利用AAS得到△AMO≌△ONB，用对应线段相等求长度，然后过点M作MH⊥OA，易得△OMH∽△OAM，然后由相似三角形的对应边成比例，求得M点的坐标；
（3）如图，作EK⊥y轴于K点，利用AAS得到△AOB≌△BKE，利用全等三角形对应边相等得到OA=BK，EK=OB，再利用AAS得到△PBF≌△PKE，寻找相等线段，并进行转化，求得PB的长，继而求得△ABP的面积；
（4）由（3）可得OA=BK=5，EK=OB=5k，则可得OK=OB+BK=5k+5，即可得点E（-5k，5k+5），继而可知动点E在直线y=-x+5上运动．

解：(1)∵直线L：y＝mx+5m，

∴A(﹣5，0)，B(0，5m)，

由OA＝OB得,5m＝5，m＝1，

∴直线解析式为：y＝x+5．

(2)在△AMO和△OBN中，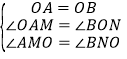

∴△AMO≌△ONB．

∴AM＝ON＝4，

∴BN＝OM＝3．

∴MN＝OM+ON＝7，

(3)如图，作EK⊥y轴于K点．

先证△ABO≌△BEK，

∴OA＝BK，EK＝OB．

再证△PBF≌△PKE，

∴PK＝PB．

∴PB＝BK＝OA．

S△ABP＝=AO2＝

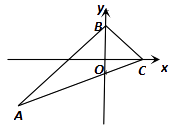
(4)如图3，∵A(﹣5，0)，B(0，5k)，

∴OA＝BK＝5，EK＝OB＝5k，

∴OK＝OB+BK＝5k+5，

∴点E(﹣5k，5k+5)，

∵动点E在直线y＝﹣x+5上运动．

故答案为：y＝﹣x+5．