��Ŀ����
����Ŀ��ij��˾����һ�ֽ���Ϊ20Ԫ/���ļ���������������y������������ۼ۸�x��Ԫ/�����ı仯���±���
�۸�x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
������y������� | �� | 5 | 4 | 3 | 2 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ��
��1���۲첢�������е�y��x֮��Ķ�Ӧ��ϵ������ѧ����һ�κ�������������������κ������й�֪ʶд��y���������x��Ԫ/�����ĺ�������ʽ��
��2������ù�˾�������ּ������ľ�����z����Ԫ�������ۼ۸�x��Ԫ/�����ĺ�������ʽ�����ۼ۸�Ϊ����Ԫʱ������������ֵ�Ƕ��٣�
��3���ù�˾Ҫ�������ܵ���40��Ԫ����д�����ۼ۸�x��Ԫ/������ȡֵ��Χ�������迼�������������ܴ����ۼ۸�Ӧ��Ϊ����Ԫ��
���𰸡�
��1���⣺���ݱ��������ݿɵó���y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b������ɵã�![]() ��
��
��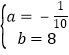 .
.
�ຯ������ʽΪ��y=-![]() x+8.
x+8.
��2���⣺��������ã�z=��x��20��y��40=��x��20���� ![]() x+8����40=
x+8����40= ![]() ��x��50��2+50��
��x��50��2+50��
�� ![]() ��0��
��0��
��x=50��z���=50.
��ù�˾�������ּ������ľ�������z����ʽΪz=-![]() x2 +10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ.
x2 +10x��200�����ۼ۸�Ϊ50Ԫ/��ʱ��������������ֵ��50��Ԫ.
��3���⣺����˾Ҫ������Ϊ40��Ԫʱ���� ![]() (x50)2 +50=40��
(x50)2 +50=40��
��ã�x1=40��x2=60��
������ͼ��IJ�ͼ��ͨ���۲캯��y= ![]() (x50)2 +50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
(x50)2 +50��ͼ��֪���չ�˾Ҫ��ʹ����������40��Ԫ�������ۼ۸��ȡֵ��ΧΪ��40��x��60��
��y��x�ĺ�����ϵʽΪ��y=-![]() x+8��y��x����������٣����迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/��.
x+8��y��x����������٣����迼�������������ܴ����ۼ۸�Ӧ��Ϊ40Ԫ/��.

����������1�����ݱ��������ݿɵó�y��x��һ�κ�����ϵ�������ʽΪ��y=ax+b��������ж�Ԫһ�η����飬��֮���ɵó���.
��2����������=ÿ������������ó�z��x�ĺ�����ϵʽ��z=��x��20��y��40=��x��20���� ![]() x+8����40=
x+8����40= ![]() ��x��50��2+50�����ݺ������ʼ��ɵó���.
��x��50��2+50�����ݺ������ʼ��ɵó���.
��3���ɣ�2���еó��ú�������ʽ����z=40���ⷽ�̼��ɵó����ۼ۸�x1=40��x2=60���迼�������������ܴ����ɺ���ͼ�����ʵó����ۼ۸�Ӧ��Ϊ40Ԫ/��.
�����㾫��������һ�κ��������ʺͶ��κ����������ǽ����ĸ�������Ҫ֪��һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�