题目内容
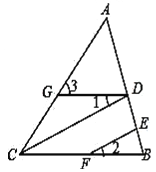
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.
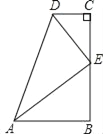
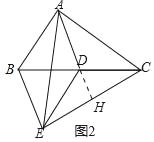
灵活应用:如图2,△ABC中,∠BAC=90°,AB=6,AC=8,点D是BC的中点,连接AD,将△ACD沿AD翻折得到△AED,连接BE,CE.
(1)填空:AD= ;
(2)求证:∠BEC=90°;
(3)求BE.

【答案】(1)5;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用勾股定理求出BC,再利用阅读理解中的结论即可解决问题;
(2)由将△ACD沿AD翻折得到△AED,推出CD=DE=BD,推出∠DBE=∠DEB,∠DCE=∠DEC,由∠DBF+∠DEB+∠DEC+∠DCE=180°,推出2∠DEB+2∠DEC=180°,可得∠DEB+∠DEC=90°;
(3)如图2中,延长AD交EC于H.由△ACB∽△HAC,![]() =
=![]() ,求出AH,DH,再证明BE=2DH即可解决问题;
,求出AH,DH,再证明BE=2DH即可解决问题;
(1)解:在Rt△ABC中,∵∠BAC=90°,AB=6,AC=8,
∴BC=![]() =10,
=10,
∵BD=DC,
∴AD=![]() BC=5,
BC=5,
故答案为5;
(2)证明:∵将△ACD沿AD翻折得到△AED,
∴CD=DE=BD,
∴∠DBE=∠DEB,∠DCE=∠DEC,
∵∠DBF+∠DEB+∠DEC+∠DCE=180°,
∴2∠DEB+2∠DEC=180°,
∴∠DEB+∠DEC=90°,
∴∠BEC=90°;
(3)解:如图2中,延长AD交EC于H.
∵AE=AE,∠HAE=∠HAC,
∴AH⊥EC,
∴EH=CH,
∵BD=CD,
∴BE=2DH,
∵DA=DC,
∴∠ACB=∠CAH,
∵∠CAB=∠AHC=90°,
∴△ACB∽△HAC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AH=![]() ,
,
∴DH=AH﹣AD=![]() ﹣5=
﹣5=![]() ,
,
∴BE=2DH=![]() .
.