题目内容
【题目】如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为: y=![]() x1 ,则tanA的值是 .
x1 ,则tanA的值是 . 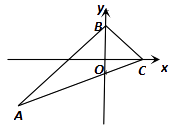
【答案】![]()
【解析】∵△ABC的内心在y轴上,
∴∠ABO=∠CBO,
又∵C(2,0),B(0,2),
∴BO=CO,BC=2![]() ,
,
∴∠BCO=∠CBO=45°,
∴∠ABC=90°,
又∵直线AC的解析式为: y=![]() x1 ,
x1 ,
∴设A(x,![]() x1 ),
x1 ),
∴AB2=x2+(![]() x3)2,AC2=(x-2)2+(
x3)2,AC2=(x-2)2+(![]() x1 )2,
x1 )2,
∴AB2+BC2=AC2,
∴x2+(![]() x3)2+8=(x-2)2+(
x3)2+8=(x-2)2+(![]() x1 )2,
x1 )2,
∴x=-6,
∴y=-4,
∴A(-6,-4),
∴AB=6![]() ,
,
∴tanA=![]() =
=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】利用勾股定理的概念和锐角三角函数的定义对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
相关题目