Question

【题目】如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．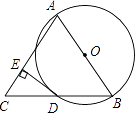

（1）求证：DE为⊙O的切线；
（2）若⊙O的半径为5，∠BAC=60°，求DE的长．

Answer 1

【答案】
（1）证明：如图，连接OD．

∵OA=OB，CD=BD，

∴OD∥AC．

∴∠ODE=∠CED．

又∵DE⊥AC，

∴∠CED=90°．

∴∠ODE=90°，即OD⊥DE．

∴DE是⊙O的切线

（2）解：∵OD∥AC，∠BAC=60°，

∴∠BOD=∠BAC=60°，

∠C=∠0DB．

又∵OB=OD，

∴△BOD是等边三角形．

∴∠C=∠ODB=60°，

CD=BD=5．

∵DE⊥AC，

∴DE=CDsin∠C=5×sin60°= ．

【解析】要证明直线与圆相切，常添加的辅助线是“作垂直，证半径”或“连半径证垂直”（1）要证DE为⊙O的切线；因为点D在⊙O上，所以添加的辅助线是“连半径证垂直”，由此连接OD，抓住已知条件点D是线段BC的中点，点O是AB的中点根据三角形中位线的定义及定理，可证得OD∥AC，由DE⊥AC，可得到OD⊥DE，即可得出结论；（2）由（1）的证明过程可以知道OD∥AC，又有∠BAC=60°，易证△BOD是等边三角形，即可得到BD、CD的长，再根据锐角三角形函数或勾股定理可以求得DE的长。