Question

【题目】画出二次函数的图象．

（1）利用图象求方程的近似很（结渠精确到）；

（2）设该抛物线的顶点为M，它与直线y=－3的两个交点分别为C、D，求△MCD的面积．

Answer 1

【答案】（1）x=1.4或3.4；（2）；

【解析】

（1）根据函数与方程的关系，可得函数图象与x轴的交点的横坐标就是相应的方程的解．

（2）解方程x2-2x-5=-3，根据根与系数的关系得出x1+x2=2，x1x2=-2，因为抛物线与直线y=-3的两个交点C、D的横坐标就是方程的两个根，所以进而求得CD=|x1-x2|=

，然后根据三角形的面积公式求得即可．

方程x22x5=0根是函数y=x22x5与x轴交点的横坐标。

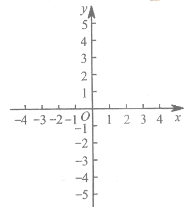
作出二次函数y=x22x5的图象，如图所示，

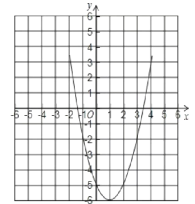
(1)由图象可知方程有两个根，一个在2和1之间，另一个在3和4之间.

先求2和1之间的根，

当x=1.4时，y=0.24；当x=1.5时，y=0.25；

因此，x=1.4是方程的一个近似根，

同理，x=3.4是方程的另一个近似根.

故一元二次方程x22x5=0的近似根为x=1.4或3.4.

(2)根据题意,得x22x5=3，

整理得x22x2=0，

∴x1+x2=2,x1x2=2，

∴CD=|x1x2|=

∴在△CDM中,S△CDM=

∴三角形CDM的面积是.