题目内容
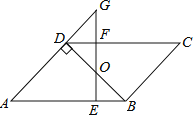
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
【答案】![]() 或
或![]()
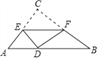
【解析】分析:若△CEF与△ABC相似,分两种情况:①若若CE:CF=3:4,如图1所示,此时EF∥AB. CD为AB边上的高,②若CF:CE=3:4,如图2所示.由相似三角形角之间的关系,可以推出∠A=∠ECD,与∠CEF=∠B.从而得到![]() ,即D点为AB的中点.
,即D点为AB的中点.
详解:若△CEF与△ABC相似,分两种情况:
若CE:CF=3:4,如图1所示:

∵CE:CF=AC:BC,
∴EF∥AB.
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高,
在Rt△ABC中,∵![]()
∴![]()
∴![]()
∴AD=ACcosA=![]()
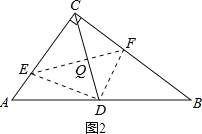
若CF:CE=3:4,如图2所示:
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,![]()
又∵![]()
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D点为AB的中点,
∴![]()
综上所述,AD的长为![]() 或
或![]()
故答案为:![]() 或
或![]()

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】2020年1月的日历表如表所示:
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
快到放寒假了,班主任孙老师看日历届时准备安排一节假期安全班会课,孙老师把日历与本学期书本上73页的数学活动3联系在一起,经过思索后,孙老师给孩子们展示两个问题:
(1)若连续三天的号数之和等于48,那么这三天分别是几号?
(2)用一个“T”字形的框在表中框出四个数,这四个数的和能等于83吗?为什么?