题目内容
【题目】如图,图1、图2、图3、…图n分别是⊙O的内接正三角形ABC,正四边形ABCD,正五边形ABCDE,、…、正n边形ABCD…,点M、N分别从点B,C开始以相同的速度在⊙O上逆时针运动.
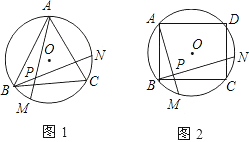
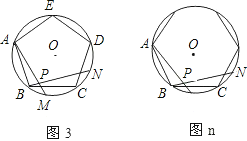
(1)求图1中∠APN的度数;
(2)求图2中,∠APN的度数,求图3中∠BPN的度数;
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
【答案】(1)∠APN=60°;(2)90°;108°;(3)![]() .
.
【解析】
(1)由△ABC为等边三角形可知∠ABC=60°,再由等速运动可得到∠ABP=∠NBC,再利用外角的性质可得∠APN=∠ABP+∠BAP,代换可得到∠APN=∠ABC,可求得∠APN的度数;
(2)和(1)同理可得到∠APN的度数和∠ABC的度数相等,图③中∠APN的度数和∠ABC的度数相等;
(3)结合(1)(2)可得到∠APN的度数等于多边形的内角的度数,可得到结论.
(1)图1:∵点M、N分别从点B. C开始以相同的速度在O上逆时针运动,
∴劣弧BM=劣弧CN
∴∠BAM=∠CBN,
∵∠APN=∠BPM,
∴∠APN=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
(2)同理:图2中,∠APN=∠ABC=90°;图3中,∠APN=∠ABC=108°;
(3)由(1)、(2)可知,
60°=![]() ,90°=
,90°=![]() ,108°=
,108°=![]() ,
,
∴∠APN=它所在的正多边形的内角度数,
∴在图n中,∠APN=![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | 27 |
C | 10000<x≤15000 | m |
D | 15000<x≤20000 | 33 |
E | x>20000 | 30 |
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有 户,表中m= ;
(2)请说明本次调查数据的中位数落在哪一组?
(3)在扇形统计图中,D组所在扇形的圆心角为多少度?
(4)这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?