Question

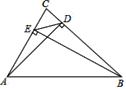
【题目】在平面直角坐标系xOy中，直线的图象经过（1，0），（－2，3）两点，且与y轴交于点A。

（1）求直线的表达式；

（2）过点A做平行于x轴的直线l，l与抛物线（a>0）交于B，C两点。若BC≥4，求a的取值范围；

（3）设直线与抛物线交于D，E两点，当3≤DE≤5时，结合函数的图象，直接写出m的取值范围是____________________。

Answer 1

【答案】（1）y=－x+1；（2）0<a≤；（3）－4≤m≤0.

【解析】

（1）利用待定系数法求函数的解析式即可求解，
（2）依题意画出图形，结合二次函数的开口大小规律可求出a的取值范围，
（3）依题意，联立方程组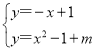 ，消去y得x2+x+m-2=0，设D（x1，y1），E（x2，y2），由DE==以及x1+x2=-1，x1x2=m-2，y1+y2=3，y1y2=m，列出方程即可解决问题．

解：（1）因为直线的图象经过（1，0），（－2，3）两点，

所以解得

所以直线y=kx+b的表达式为y=－x+1．

（2）如图所示：

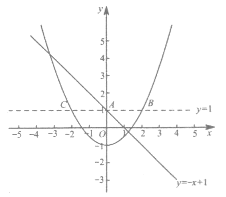
直线y=1与抛物线G1：y=ax2－1（a>0）的交点B，C关于y轴对称．

所以当线段BC的长等于4时，B，C两点的坐标分别为（2，1），（－2，1），

把点B代入y=ax2-1，1=4a-1，
解得，

所以，由抛物线二次项系数的性质及已知a>0可知，

当BC≥4时，0<a≤．

（3）依题意，联立方程组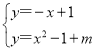，消去y得x2+x+m-2=0，

设D（x1，y1），E（x2，y2），
∴DE==

∵x1+x2=-1，x1x2=m-2，y1+y2=3，y1y2=m，
∴DE=，
当DE=3时，=3，解得m=0，
当DE=5时，=5，解得m=-4，
∴－4≤m≤0．

故答案为：（1）y=－x+1；（2）0<a≤；（3）－4≤m≤0.