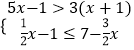Question

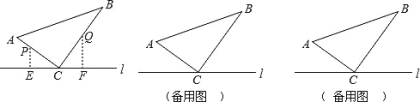
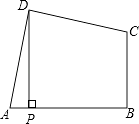
【题目】已知BC＝5，AB＝1，AB⊥BC，射线CM⊥BC，动点P在线段BC上（不与点B，C重合），过点P作DP⊥AP交射线CM于点D，连接AD．

（1）如图1，若BP＝4，判断△ADP的形状，并加以证明．

（2）如图2，若BP＝1，作点C关于直线DP的对称点C′，连接AC′．

①依题意补全图2；

②请直接写出线段AC′的长度．

Answer 1

【答案】（1）△ADP是等腰直角三角形．证明见解析；（2）①补图见解析；②

【解析】

（1）先判断出PC=AB，再用同角的余角相等判断出∠APB=∠PDC，得出△ABP≌△PCD（AAS），即可得出结论；

（2）①利用对称的性质画出图形；

②过点C'作C'Q⊥BA交BA的延长线于Q，先求出CP=4，AB=AP，∠CPD=45°，进而得出C'P=CP=4，∠C'PD=∠CPD=45°，再判断出四边形BQC'P是矩形，进而求出AQ=BQ﹣AB=3，最后用勾股定理即可得出结论．

（1）△ADP是等腰直角三角形．证明如下：

∵BC=5，BP=4，∴PC=1．

∵AB=1，∴PC=AB．

∵AB⊥BC，CM⊥BC，DP⊥AP，∴∠B=∠C=90°，∠APB+∠DPC=90°，∠PDC+∠DPC=90°，∴∠APB=∠PDC．

在△ABP和△PCD中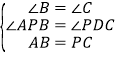，∵，∴△ABP≌△PCD（AAS），∴AP=PD．

∵∠APD=90°，∴△ADP是等腰直角三角形．

（2）①依题意补全图2；

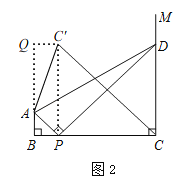
②过点C'作C'Q⊥BA交BA的延长线于Q．

∵BP=1，AB=1，BC=5，∴CP=4，AB=AP．

∵∠ABP=90°，∴∠APB=45°．

∵∠APD=90°，∴∠CPD=45°，连接C'P．

∵点C与C'关于DP对称，∴C'P=CP=4，∠C'PD=∠CPD=45°，∴∠CPC'=90°，∴∠BPC'=90°，∴∠Q=∠ABP=∠BPC'=90°，∴四边形BQC'P是矩形，∴C'Q=BP=1，BQ=C'P=4，∴AQ=BQ﹣AB=3．在Rt△AC'Q中，AC′．