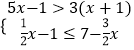Question

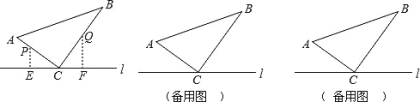
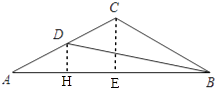
【题目】如图，已知在△ABC中，∠ABC=30°，BC=8，sin∠A= ，BD是AC边上的中线．求：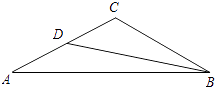

（1）△ABC的面积；
（2）∠ABD的余切值．

Answer 1

【答案】
（1）解：如图，过点C作CE⊥AB与点E，

∴BE=BCcos∠ABC=8× =4 ，

CE=BCsin∠ABC=8× =4，

在Rt△ACE中，∵sin∠A= ，

∴AC= = =4 ，

∴AE= = =8，

则AB=AE+BE=8+4 ，

故S△ABC= ABCE= ×（8+4 ）×4=16+8

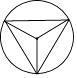
（2）解：过点D作DH⊥AB与点H，

∵CE⊥AB，

∴DH∥CE，

又∵D是AC中点，

∴AH=HE= AE=4，DH= CE=2，

∴在Rt△BDH中，cot∠ABD= = =2 +2

【解析】（1）过点C作CE⊥AB与点E，在Rt△BCE中，∵BC=8，∠ABC=30°， 解Rt△BCE得出，BE=BCcos∠ABC，CE=BCsin∠ABC，在Rt△ACE中，由sin∠A的值表示出AC的长，根据勾股定理得出AE的长，从而得出S△ABC；（2）过点D作DH⊥AB与点H，根据平行线的判定得出DH∥CE，再根据中位线得判定得出AH=HE =4，DH =2，在Rt△BDH中，得出cot∠ABD的值。
【考点精析】根据题目的已知条件，利用平行线的判定与性质和三角形中位线定理的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．