题目内容
【题目】平面直角坐标系中,点A坐标为(a,0),点B坐标为(b,2),点C坐标为(c,m),其中a、b、c满足方程组![]() .
.

(1)若a=2,则三角形AOB的面积为 ;
(2)若点B到y轴的距离是点C到y轴距离的2倍,求a的值;
(3)连接AB、AC、BC,若三角形ABC的面积小于等于9,求m的取值范围.
【答案】(1)2;(2)a=11或a=![]() ;(3)﹣
;(3)﹣![]() 且m≠﹣
且m≠﹣![]() .
.
【解析】
(1)求出A点坐标,可求出答案;
(2)由题意得出b=a+3,c=a-4,则B(a+3,2),C(a-4,m),则|a+3|=2|a-4|,解方程即可得出答案;
(3)过点C作y轴的平行线l,延长BA交l于M,过点B作x轴的平行线交直线l于点D,直线l交x轴于点E,由面积法得M(a﹣4,﹣![]() ),根据S△BCM-S△ACM≤9,可得出关于a的不等式组,则可得出答案.
),根据S△BCM-S△ACM≤9,可得出关于a的不等式组,则可得出答案.
(1)∵点A坐标为(a,0),点B坐标为(b,2),a=2,
∴A(2,0),
∴三角形AOB的面积为![]() ×2×2=2;
×2×2=2;
故答案为:2;
(2)∵a、b、c满足方程组![]() .
.
∴b=a+3,c=a﹣4,
∴B(a+3,2),C(a﹣4,m),
∵点B到y轴的距离是点C到y轴距离的2倍,
∴|a+3|=2|a﹣4|,
∴a=11或a=![]() ;
;
(2)过点C作y轴的平行线l,延长BA交l于M,过点B作x轴的平行线交直线l于点D,直线l交x轴于点E,
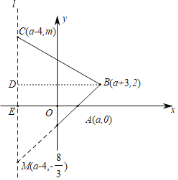
设EM=n,则BD=7,DE=2,AE=4,
∵S△BDM=S△AEM+S梯形BDEA,
∴![]() ×7×(2+n)=
×7×(2+n)=![]() ×4×n+
×4×n+ ![]() ×2×(4+7),
×2×(4+7),
解得:n=![]() ,
,
∴M(a﹣4,﹣![]() ),
),
∵S△ABC≤9,
∴S△BCM﹣S△ACM≤9,
∴![]() |,
|,![]() |≤6,
|≤6,
∴![]() ,
,
∵m≠﹣![]() ,
,
∴![]() 且m≠﹣
且m≠﹣![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目