题目内容
【题目】请将下列证明过程补充完整:
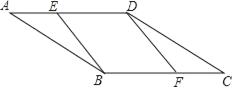
已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
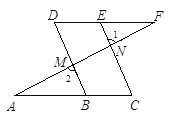
求证:∠C=∠D.
证明:因为∠1=∠2(已知),
又因为∠1=∠ANC( ),
所以 (等量代换).
所以 ∥ (同位角相等,两直线平行),
所以∠ABD=∠C( ).
又因为∠A=∠F(已知),
所以 ∥ ( ).
所以 (两直线平行,内错角相等).
所以∠C=∠D( ).
【答案】见解析.
【解析】
根据对顶角相等,可得∠1=∠ANC,然后由∠1=∠2,根据等量代换可得∠2=∠ANC,再结合平行线的性质与判定可完成填空.
证明:因为∠1=∠2(已知),
又因为![]() ( 对顶角相等 ),
( 对顶角相等 ),
所以∠2=∠ANC (等量代换).
所以 BD ∥ EC (同位角相等,两直线平行),
所以![]() ( 两直线平行,同位角相等 ).
( 两直线平行,同位角相等 ).
又因为![]() (已知),
(已知),
所以 AC ∥ DF ( 内错角相等,两直线平行 ).
所以 ∠D=∠DBA (两直线平行,内错角相等).
所以![]() ( 等量代换 )
( 等量代换 )

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目