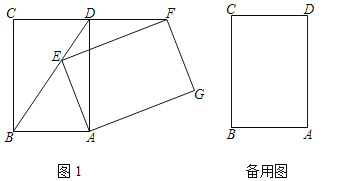
题目内容
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地后立即以另一速度按原路匀速返回到
地后立即以另一速度按原路匀速返回到![]() 地; 乙车匀速前往
地; 乙车匀速前往![]() 地,设甲、乙两车距
地,设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() 时),
时), ![]() 与
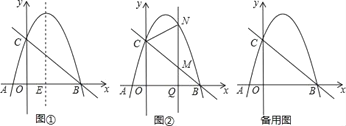
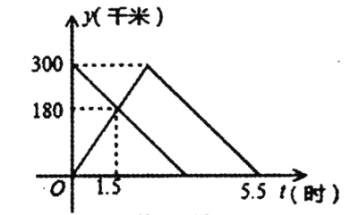
与![]() 之间的函数图象如图所示
之间的函数图象如图所示
(1)甲车从![]() 地到
地到![]() 地的速度是__________千米/时,乙车的速度是__________千米/时;
地的速度是__________千米/时,乙车的速度是__________千米/时;
(2)求甲车从![]() 地到达
地到达![]() 地的行驶时间;
地的行驶时间;
(3)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)求乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程.
地的路程.
【答案】(1)![]() ;
;
(2)甲车从![]() 地到达
地到达![]() 地的行驶时间是2.5小时;
地的行驶时间是2.5小时;
(3)甲车返回时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]() ;
;
(4)乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程是175千米.
地的路程是175千米.
【解析】
(1)根据题意列算式计算即可得到结论;
(2)根据题意列算式计算即可得到结论;
(3)设甲车返回时![]() 与
与![]() 之间的函数关系式为y=kt+b,根据题意列方程组求解即可得到结论;
之间的函数关系式为y=kt+b,根据题意列方程组求解即可得到结论;
(4)根据题意列算式计算即可得到结论.
解:(1)甲车从A地开往B地时的速度是:180÷1.5=120千米/时,乙车从B地开往A地的速度是:(300-180)÷1.5=80千米/时,
故答案为:120;80;
(2)![]() (小时)
(小时)
答:甲车从![]() 地到达
地到达![]() 地的行驶时间是2.5小时
地的行驶时间是2.5小时
(3)设甲车返回时![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,
,
则有![]()
解得:![]() ,
,
∴甲车返回时![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]()
(4)![]() 小时,
小时,
把![]() 代入
代入![]() 得:
得:![]()
答:乙车到达![]() 地时甲车距
地时甲车距![]() 地的路程是175千米.
地的路程是175千米.

 天天练口算系列答案
天天练口算系列答案【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户一个月用了
时,某用户一个月用了![]() 水,求该用户这个月应缴纳的水费;
水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为![]() 立方米,当
立方米,当![]() 时,求该用户应缴纳的水费(用含
时,求该用户应缴纳的水费(用含![]() 、
、![]() 的整式表示);
的整式表示);
(3)当![]() 时,甲、乙两用户一个月共用水
时,甲、乙两用户一个月共用水![]() .已知甲用户用水量超过了
.已知甲用户用水量超过了![]() ,设甲用户这个月用水如
,设甲用户这个月用水如,试求甲、乙两用户一个月共缴纳的水费.(用含
![]() 的整式表示)
的整式表示)
【题目】小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示:
1次 | 2次 | 3次 | 4次 | 5次 | |
小明 | 10 | 14 | 13 | 12 | 13 |
小兵 | 11 | 11 | 15 | 14 | 11 |
根据以上信息,解决以下问题:
(1)小明成绩的中位数是__________.
(2)小兵成绩的平均数是__________.
(3)为了比较他俩谁的成绩更稳定,老师利用方差公式计算出小明的方差如下(其中![]() 表示小明的平均成绩);
表示小明的平均成绩);
![]()
请你帮老师求出小兵的方差,并比较谁的成绩更稳定。