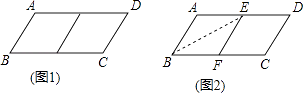题目内容
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
【答案】
(1)证明略
(2)等腰三角形,理由略
【解析】(本小题满分8分)
证明:(1)∵BE=CF,
∴BE+EF=CF+EF, …………1分
即BF=CE. …………………2分
又∵∠A=∠D,∠B=∠C,
∴△ABF≌△DCE(AAS), ……………………………………4分
∴AB=DC. ………………………………………5分
(2)△OEF为等腰三角形 …………………………………6分
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC.
∴OE=OF.
∴△OEF为等腰三角形. …………………………………8分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了解某品牌A,B两种型号冰箱的销售情况,王明对某专卖店一到七月份的销售情况进行了统计,并将得到的数据制成如下统计表:
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
A型销 售量(台) | 10 | 14 | 17 | 16 | 13 | 14 | 14 |
B型销 售量(台) | 6 | 10 | 14 | 15 | 16 | 17 | 20 |
完成下表:
平均数(台) | 中位数(台) | 方差 | |
A型销售量 | 14 | ||
B型销售量 | 14 | 18.6 |