题目内容
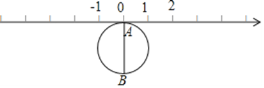
【题目】如图,数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,a、c满足![]() .AB表示点A、B之间的距离,且
.AB表示点A、B之间的距离,且![]() .
.
![]()
(1)![]() ________,
________,![]() ________;
________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数________表示的点重合;
(3)点A、B、C在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则![]() ________,
________,![]() ________.(用含t的代数式表示)
________.(用含t的代数式表示)
(4)在(3)的条件下,请问:![]() 的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
的值是否随着时间t的变化而改变?若变化,请说明理由,若不变,请求其值.
【答案】(1)-3,1;(2)4;(3)![]() ,
,![]() ;(4)3BC-2AB=-4t-1,故3BC-2AB的值随时间t值的变化而变化
;(4)3BC-2AB=-4t-1,故3BC-2AB的值随时间t值的变化而变化
【解析】
(1)根据![]() ,得到a=-3,c=8,由b是最小的正整数得到b=1;(2)将数轴折叠,使得A点与C点重合,即点A与点C关于数2.5表示的点对称,故点B与数4表示的点对称;(3)根据点运动方向及速度即可表示AC、BC;(4)计算
,得到a=-3,c=8,由b是最小的正整数得到b=1;(2)将数轴折叠,使得A点与C点重合,即点A与点C关于数2.5表示的点对称,故点B与数4表示的点对称;(3)根据点运动方向及速度即可表示AC、BC;(4)计算![]() =-4t-1,故
=-4t-1,故![]() 的值随t的变化而变化.
的值随t的变化而变化.
解:(1)∵![]() ,
,
∴a+3=0,c-8=0,
∴a=-3,c=8,
∵b是最小的正整数,
∴b=1,
故填-3,1;
(2)点A与点C的中点表示的数是![]() ,
,
∴![]() ,
,
∴点B与数4表示的点重合;
(3)由题意知AC=8-(-3)=11,BC=8-1=7,
∴t秒后AC=![]() ,BC=
,BC=![]() ,
,
故填5t+11,2t+7;
(4)![]()
=![]() ,
,
![]() ,
,
=-4t-1.
故![]() 的值随t的变化而变化.
的值随t的变化而变化.

【题目】小明和小兵两人参加体育项目训练,近期的5次测试成绩如下表所示:
1次 | 2次 | 3次 | 4次 | 5次 | |
小明 | 10 | 14 | 13 | 12 | 13 |
小兵 | 11 | 11 | 15 | 14 | 11 |
根据以上信息,解决以下问题:
(1)小明成绩的中位数是__________.
(2)小兵成绩的平均数是__________.
(3)为了比较他俩谁的成绩更稳定,老师利用方差公式计算出小明的方差如下(其中![]() 表示小明的平均成绩);
表示小明的平均成绩);
![]()
请你帮老师求出小兵的方差,并比较谁的成绩更稳定。